Chemists in the late 1800s knew that cyclic molecules existed, but the limitations on ring size were unclear. Although numerous compounds containing five-membered and six-membered rings were known, smaller and larger ring sizes had not been prepared, despite many attempts.

A theoretical interpretation of this observation was proposed that suggested small and large rings might be unstable due to angle strain—the strain induced in a molecule when bond angles are forced to deviate from the ideal 109° tetrahedral value. This proposal was based on the simple geometric notion that a three-membered ring (cyclopropane) should be an equilateral triangle with bond angles of 60° rather than 109°, a four-membered ring (cyclobutane) should be a square with bond angles of 90°, a five-membered ring should be a regular pentagon with bond angles of 108°, and so on. Continuing this argument, large rings should be strained by having bond angles that are much greater than 109°.

What are the facts? To measure the amount of strain in a compound, we have to measure the total energy of the compound and then subtract the energy of a strain-free reference compound. The difference between the two values should represent the amount of extra energy in the molecule due to strain. The simplest experimental way to do this for a cycloalkane is to measure its heat of combustion, the amount of heat released when the compound burns completely with oxygen. The more energy (strain) the compound contains, the more energy (heat) is released by combustion.

(CH₂)_“ + 3𝑛/2 O₂ → 𝑛 CO₂ + 𝑛 H₂O + Heat

Because the heat of combustion of a cycloalkane depends on size, we need to look at heats of combustion per CH₂ unit. Subtracting a reference value derived from a strain-free acyclic alkane and then multiplying by the number of CH₂ units in the ring gives the overall strain energy. Figure 4.4 shows the results.

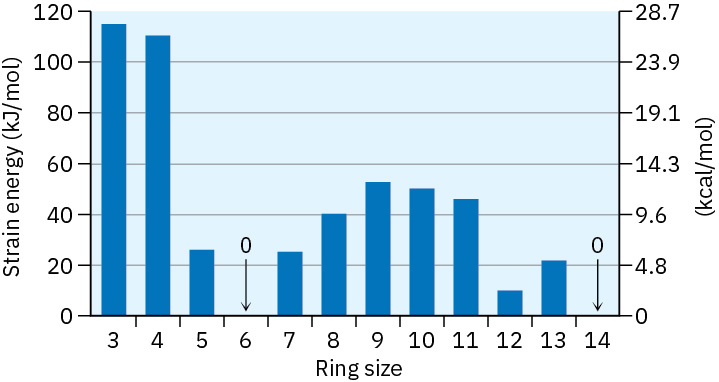
Figure 4.4 Cycloalkane strain energies, as calculated by taking the difference between cycloalkane heat of combustion per CH₂ and acyclic alkane heat of combustion per CH₂, and multiplying by the number of CH₂ units in a ring. Small and medium rings are strained, but cyclohexane rings and very large rings are strain-free.

The data in Figure 4.4 show that cyclopropane and cyclobutane are indeed strained, just as predicted, but cyclopentane is more strained than predicted, and cyclohexane is strain-free. Cycloalkanes of intermediate size have only modest strain, and rings of 14 carbons or more are strain-free. So why is the initial theory wrong? It is wrong for the simple reason that it assumed all cycloalkanes to be flat. In fact, as we’ll see in the next section, most cycloalkanes are not flat; instead, they adopt puckered three-dimensional conformations that allow bond angles to be nearly tetrahedral. As a result, angle strain occurs only in three- and four-membered rings, which have little flexibility. For most ring sizes, particularly the medium-ring (C₇–C₁₁) cycloalkanes, torsional strain caused by H ⟷ H eclipsing interactions at adjacent carbons (Section 3.6) and steric strain caused by the repulsion between nonbonded atoms that approach too closely (Section 3.7) are the most important factors. Thus, three kinds of strain contribute to the overall energy of a cycloalkane.

• Angle strain—the strain due to expansion or compression of bond angles
• Torsional strain—the strain due to eclipsing of bonds between neighboring atoms
• Steric strain—the strain due to repulsive interactions when atoms approach each other too closely

Problem 4-8

Each H ⟷ H eclipsing interaction in ethane costs about 4.0 kJ/mol. How many such interactions are present in cyclopropane? What fraction of the overall 115 kJ/mol (27.5 kcal/mol) strain energy of cyclopropane is due to torsional strain?

Problem 4-9

cis-1,2-Dimethylcyclopropane has more strain than trans-1,2-dimethylcyclopropane. How can you account for this difference? Which of the two compounds is more stable?