Propane, another member in the alkane series, also has a torsional barrier that results in hindered rotation around the carbon–carbon bonds. The barrier is slightly higher in propane than in ethane—a total of 14 kJ/mol (3.4 kcal/mol) versus 12 kJ/mol.

The eclipsed conformation of propane has three interactions—two hydrogen–hydrogen interactions and one additional hydrogen–methyl interaction. Since each eclipsing hydrogen-hydrogen interaction is the same as that in ethane and thus has an energy “cost” of 4.0 kJ/mol, we can assign a value of 14 – (2 × 4.0) = 6.0 kJ/mol (1.4 kcal/mol) to the eclipsing hydrogen-methyl interaction (Figure 3.9).

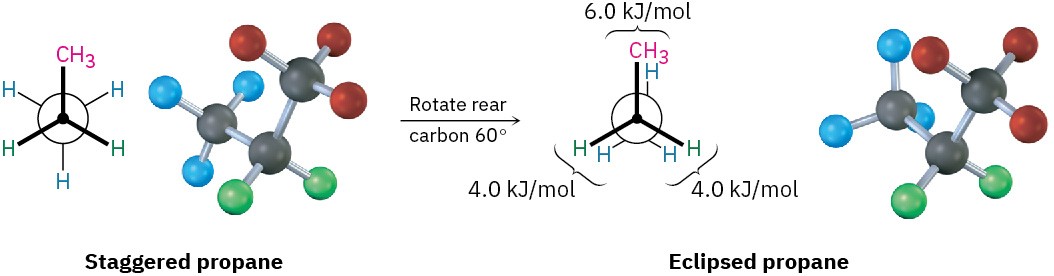
Figure 3.9 Newman projections of propane showing staggered and eclipsed conformations. The staggered conformer is lower in energy by 14 kJ/mol.

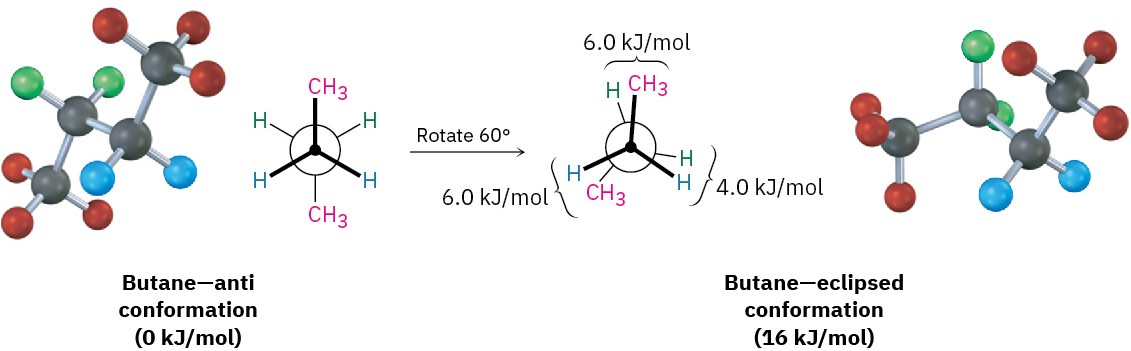
The conformational situation becomes more complex for larger alkanes because not all staggered conformations have the same energy and not all eclipsed conformations have the same energy. In butane, for instance, the lowest-energy arrangement, called the anti conformation, is the one in which the two methyl groups are as far apart as possible—having a dihedral angle of 180°. As rotation around the C2–C3 bond occurs, an eclipsed conformation is reached where there are two hydrogen-methyl interactions and one hydrogen-hydrogen interaction. Using the energy values derived previously from ethane and propane, this eclipsed conformation is more strained than the anti conformation by 2 × 6.0 kJ/mol + 4.0 kJ/mol (two hydrogen-methyl interactions plus one hydrogen-hydrogen interaction), for a total of 16 kJ/mol (3.8 kcal/mol).

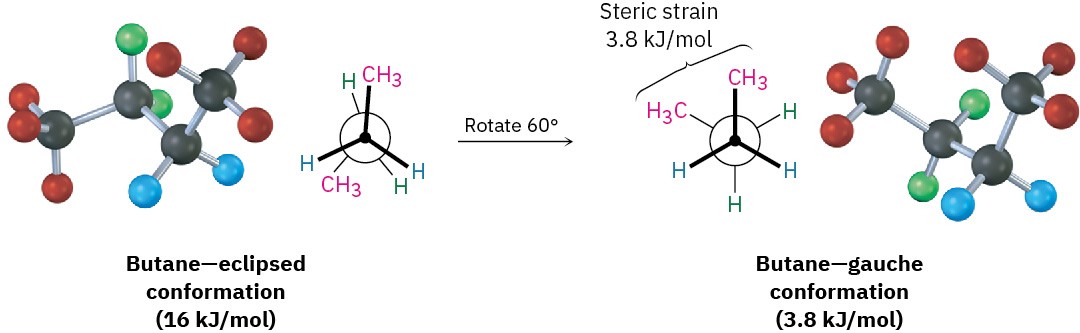
As bond rotation continues, an energy minimum is reached at the staggered conformation where the methyl groups are 60° apart. Called the gauche conformation, it lies 3.8 kJ/mol (0.9 kcal/mol) higher in energy than the anti conformation even though it has no eclipsing interactions. This energy difference occurs because the hydrogen atoms of the methyl groups are near one another in the gauche conformation, resulting in what is called steric strain. Steric strain is the repulsive interaction that occurs when atoms are forced closer together than their atomic radii allow. It’s the result of trying to force two atoms to occupy the same space.

As the dihedral angle between the methyl groups approaches zero, an energy maximum is reached at a second eclipsed conformation. Because the methyl groups are forced even closer together than in the gauche conformation, both torsional strain and steric strain are present. A total strain energy of 19 kJ/mol (4.5 kcal/mol) has been estimated for this conformation, making it possible to calculate a value of 11 kJ/mol (2.6 kcal/mol) for the methyl-methyl eclipsing interaction: total strain of 19 kJ/mol minus the strain of two hydrogen-hydrogen eclipsing interactions (2 × 4.0 kcal/mol) equals 11 kJ/mol.

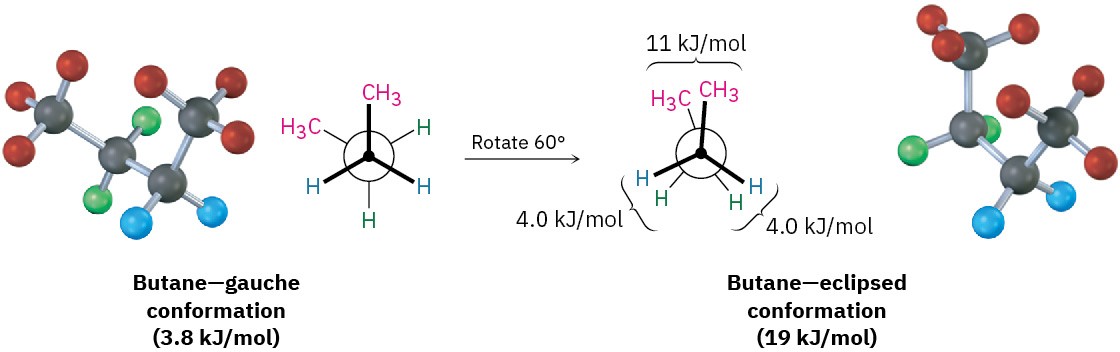
After 0°, the rotation becomes a mirror image of what we’ve already seen: another gauche conformation is reached, another eclipsed conformation, and finally a return to the anti conformation. A plot of potential energy versus rotation about the C2–C3 bond is shown in Figure 3.10.

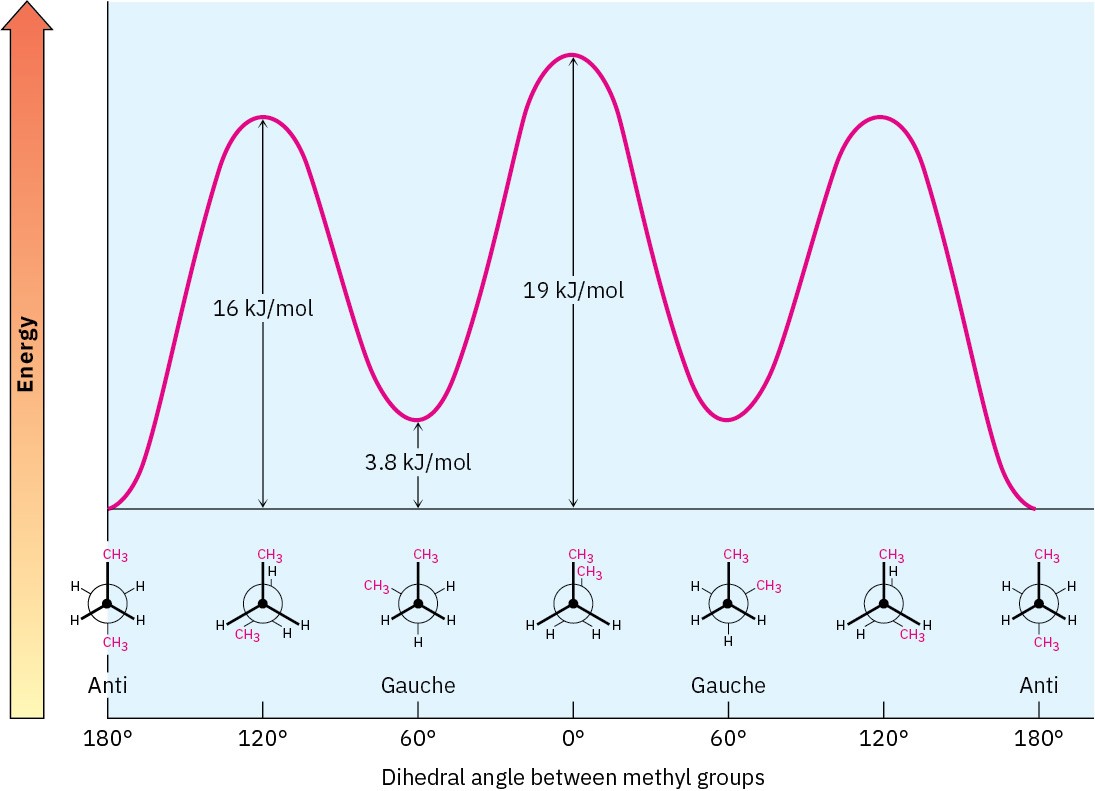
Figure 3.10 A plot of potential energy versus rotation for the C2−C3 bond in butane. The energy maximum occurs when the two methyl groups eclipse each other, and the energy minimum occurs when the two methyl groups are 180° apart (anti).

The notion of assigning definite energy values to specific interactions within a molecule is very useful, and we’ll return to it in the next chapter. A summary of what we’ve seen thus far is given in Table 3.5.

Table 3.5 Energy Costs for Interactions in Alkane Conformers

The same principles just developed for butane apply to pentane, hexane, and all larger alkanes. The most favorable conformation for any alkane has the carbon–carbon bonds in staggered arrangements, with large substituents arranged anti to one another. A generalized alkane structure is shown in Figure 3.11.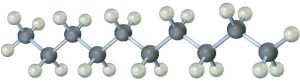

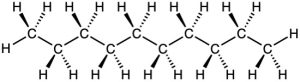
Figure 3.11 The most stable alkane conformation is the one in which all substituents are staggered and the carbon–carbon bonds are arranged anti, as shown in this model of decane.

One final point: saying that one particular conformer is “more stable” than another doesn’t mean the molecule adopts and maintains only the more stable conformation. At room temperature, rotations around σ bonds occur so rapidly that all conformers are in equilibrium. At any given instant, however, a larger percentage of molecules will be found in a more stable conformation than in a less stable one.

Worked Example 3.4 Newman Projections

Sight along the C1–C2 bond of 1-chloropropane, and draw Newman projections of the most stable and least stable conformations.

Strategy. The most stable conformation of a substituted alkane is generally a staggered one in which large groups have an anti relationship. The least stable conformation is generally an eclipsed one in which large groups are as close as possible.

Solution

Problem 3-15

Make a graph of potential energy versus angle of bond rotation for propane, and assign values to the energy maxima.

Problem 3-16

Sight along the C2–C1 bond of 2-methylpropane (isobutane).

(a) Draw a Newman projection of the most stable conformation.

(b) Draw a Newman projection of the least stable conformation.

(c) Make a graph of energy versus angle of rotation around the C2–C1 bond.

(d) Assign relative values to the maxima and minima in your graph, given that a hydrogen-hydrogen eclipsing interaction “costs” 4.0 kJ/mol and a hydrogen-methyl eclipsing interaction “costs” 6.0 kJ/mol.

Problem 3-17

Sight along the C2–C3 bond of 2,3-dimethylbutane, and draw a Newman projection of the most stable conformation.

Problem 3-18

Draw a Newman projection along the C2–C3 bond of the following conformation of 2,3-dimethylbutane, and calculate a total strain energy: