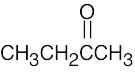12 Chapter 12 – Structure Determination: Mass Spectroscopy and Infrared Spectroscopy

Solutions to Problems

 

12.1If the isotopic masses of the atoms C, H, and O had integral values of 12 u, 1 u and 16 u, many molecular formulas would correspond to a molecular weight of 288 u. Because isotopic masses are not integral, however, only one molecular formula is associated with a molecular ion at 288.2089 u.

To reduce the number of possible formulas, assume that the difference in molecular weight between 288 and 288.2089 is due mainly to hydrogen. Divide 0.2089 by 0.00783, the amount by which the atomic weight of one ¹H atom differs from 1. The answer, 26.67, gives a “ballpark” estimate of the number of hydrogens in testosterone. Then, divide 288 by 12, to determine the maximum number of carbons. Since 288 ÷ 12 = 24, we know that testosterone can have no more than 22 carbons if it also includes hydrogen and oxygen. Make a list of reasonable molecular formulas containing C, H and O whose mass is 288 and which contain 20–30 hydrogens. Tabulate these, and calculate their exact masses using the exact atomic mass values in the text. The only possible formula for testosterone is C19H28O2.

Isotopic mass

 

Molecular formula	Mass of carbons	Mass of hydrogens	Mass of oxygens	Mass of molecular ion
C20H32O	240.0000 u	32.2504 u	15.9949 u	288.2453 u
C19H28O2	228.0000	28.2191	31.9898	288.2089
C18H24O3	216.0000	24.1879	47.9847	288.1726
12.2

Fragmentation occurs to a greater extent at the weakest carbon–carbon bonds, producing a relatively stable cation. Spectrum (a), which has a dominant peak at m/z = 69, corresponds to 2-methyl-2-pentene, and spectrum (b), which has m/z = 55 as its base peak, corresponds to 2-hexene.

 

• In a mass spectrum, the molecular ion is both a cation and a radical. When it fragments, two kinds of cleavage can occur. (1) Cleavage can form a radical and a cation (the species observed in the mass spectrum). Alpha cleavage shows this type of pattern. (2) Cleavage can form a neutral molecule and a different radical cation (the species observed

 

 

in the mass spectrum). Alcohol dehydration and the McLafferty rearrangement show this cleavage pattern.

For each compound, calculate the mass of the molecular ion and identify the functional groups present. Draw the fragmentation products and calculate their masses.

(a)

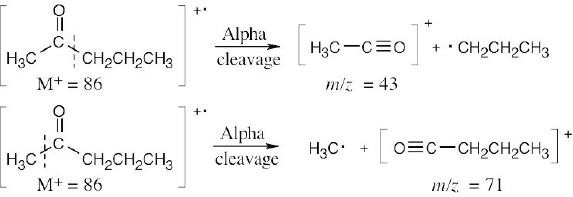
In theory, alpha cleavage can take place on either side of the carbonyl group to produce cations with m/z = 43 and m/z = 71. In practice, cleavage occurs on the more substituted side of the carbonyl group, and the first cation, with m/z = 43, is observed.

(b)

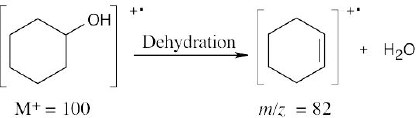
Dehydration of cyclohexanol produces a cation radical with m/z = 82.

(c)

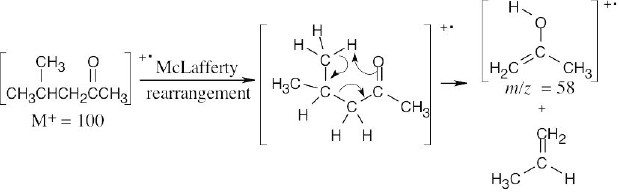
The cation radical fragment resulting from McLafferty rearrangement has m/z = 58.

(d)

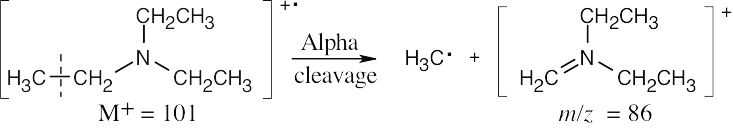
Alpha cleavage of triethylamine yields a cation with m/z = 86.

 

 

• Identify the functional groups present in the molecule and recall the kinds of fragmentations those functional groups produce. 2-Methyl-2-pentanol produces fragments that result from both dehydration and from alpha cleavage. Two different alpha cleavage products are possible.

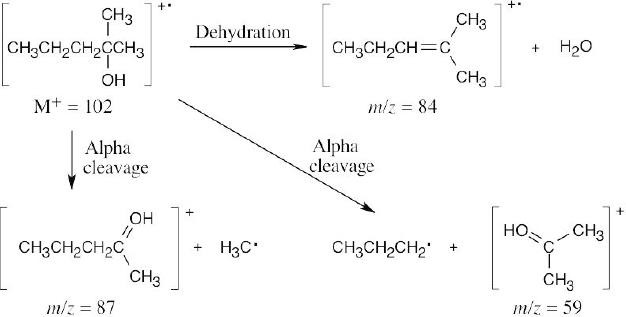
Peaks might appear at M⁺ = 102 (molecular ion), 87, 84, 59.

 

• We know that: (1) energy increases as wavelength decreases, and (2) the wavelength of X-radiation is smaller than the wavelength of infrared radiation. Thus, we estimate that an X ray is of higher energy than an infrared ray.

ε = hv = hc/λ; h = 6.62 ×10⁻³⁴ J ⋅ s; c = 3.00 ×10⁸ m/s for λ = 1×10⁻⁶ m (infrared radiation):

 

ε = (6.62 ×10⁻³⁴ J ⋅s)(3.00 ×10⁸ m/s) =×

−19

 

1.0 ×10⁻⁶ m

for λ = 3.0 ×10⁻⁹ m (X radiation):

2.0 10J

 

ε = (6.62 ×10⁻³⁴ J ⋅s)(3.00 ×10⁸ m/s) =×

−17

 

3.0 ×10⁻⁹ m

6.6 10J

 

Confirming our estimate, the calculation shows that an X ray is of higher energy than infrared radiation.

Convert radiation in m to radiation in Hz by the equation:

 

 

v = c =

λ

3.00×10⁸ m/s

 

9.0×10⁻⁶ m

= 3.3×10¹³ Hz

 

The equation ɛ = hν shows that the greater the value of ν, the greater the energy. Thus, radiation with ν = 3.3 × 10¹³ Hz (λ= 9.0 × 10^–6 m) is higher in energy than radiation with ν = 4.0 × 10⁹ Hz.

 

 

1.20 ×10⁻⁴ kJ/mol1.20 ×10⁻⁴ kJ/mol

 

• E =

λ(in m)

=5×10⁻¹¹

 

= 2.4 ×10⁶ kJ/mol for a gamma ray.

• E = 4.0 × 10⁴ kJ/mol for an X ray.

cc3.0×10⁸ m/s₋₈

(c)v =; λ === 5.0×10m

λv6.0×10¹⁵ Hz

 

1.20×10⁻⁴ kJ/mol

E =5.0×10⁻⁸

= 2.4×10³ kJ/mol for ultraviolet light.

 

• E = 2.8 × 10² kJ/mol for visible light.
• E = 6.0 kJ/mol for infrared radiation.
• E = 4.0 × 10^–2 kJ/mol for microwave radiation.

 

• (a)A compound with a strong absorption at 1710 cm^–1 contains a carbonyl group and is either a ketone or aldehyde.
• A compound with a nitro group has a strong absorption at 1540 cm^–1.
• A compound showing both carbonyl (1720 cm^–1) and –OH (2500–3000 cm^–1 broad) absorptions is a carboxylic acid.

 

• To use IR spectroscopy to distinguish between isomers, find a strong IR absorption that is present in one isomer but absent in the other.

 

 

• CH3CH2OH

Strong hydroxyl band at 3400–3640 cm^–

• CH3CH2CH2CH2CH=CH2 Alkene bands at 3020–3100 cm^–1 and at 1640–1680^–1

 

 

• CH3CH2CO2H

Strong, broad band at 2500–3100 cm^–1

CH3OCH3

No band in the region 3400– 3640 cm^–1

No bands in alkene region HOCH2CH2CHO

Strong band at 3400–3640 cm–1

 

 

• Based on what we know at this point, we can identify four absorptions in this spectrum.
• Absorptions in the region 1450 cm^–1–1600 cm^–1 are due to aromatic ring –C=C– motions.
• The absorption at 2100 cm^–1 is due to a –C≡C– stretch.
• Absorptions in the range 3000 cm^–1 – 3100 cm^–1 are due to aromatic ring =C–H stretches.
• The absorption at 3300 cm^–1 is due to a ≡C–H stretch.

 

• (a)An ester next to a double bond absorbs at 1715 cm^–1. The alkene double bond absorbs around 1640 cm^–1, and the C–O from ester absorbs at 1250 cm^–1.
• The aldehyde carbonyl group absorbs at 1730 cm^–1. The alkyne C≡C bond absorbs at 2100–2260 cm^–1, and the alkyne H–C≡ bond absorbs at 3300 cm^–1.
• The most important absorptions for this compound are due to the alcohol group (a broad, intense band at 3400–3650 cm^–1) and to the carboxylic acid group, which has a C=O absorption in the range 1710–1760 cm^–1 and a broad O–H absorption in the range 2500–3100 cm^–1. Absorptions due to the aromatic ring [3030 cm^–1 (w) and 1450–1600 cm^–1 (m)] may also be seen.

 

 

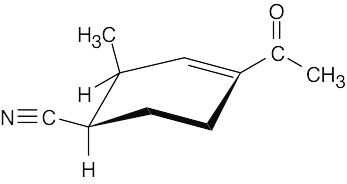
The compound contains nitrile and ketone groups, as well as a carbon–carbon double bond. The nitrile absorption occurs at 2210–2260 cm^–1. The ketone shows an absorption at 1690 cm^–1, a lower value than usual because the ketone is next to the double bond. The double bond absorption occurs at 1640–1680 cm^–1.

 

Additional Problems

 

Visualizing Chemistry

 

 

Compound

Significant

IR Absorption

Due to:

 

 

 

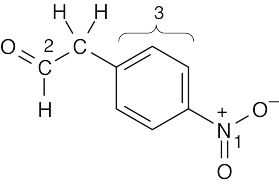(a)1540 cm^–1

1730 cm^–1

3030 cm^–1

1450–1600 cm^–1

nitro group (1)

aldehyde (2) aromatic ring C–H(3) aromatic ring C=C(3)

 

 

 

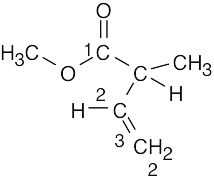(b)1735 cm^–1

3020–3100 cm^–1

 

910 cm^–1, 990 cm^–1

1640–1680 cm^–1

 

 

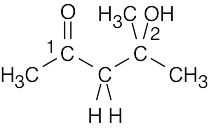(c)1715 cm^–1

3400–3650 cm^–1

ester (1)

vinylic stretch C–H(2)

 

C=CH2 bend(3) alkene C=C

 

 

ketone (1)

alcohol (2)

 

 

 

 

 

 

• (a)The mass spectrum of this ketone shows fragments resulting from both McLafferty rearrangement and alpha cleavage.

McLafferty rearrangement:

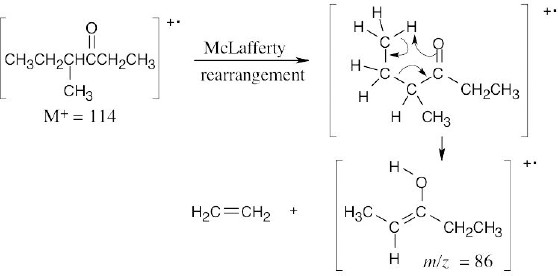
Alpha cleavage:

 

 

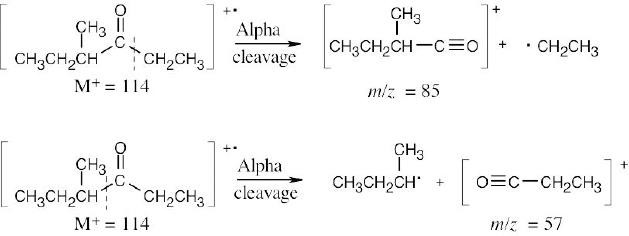
(b)Two different fragments can arise from alpha cleavage of this amine:

 

 

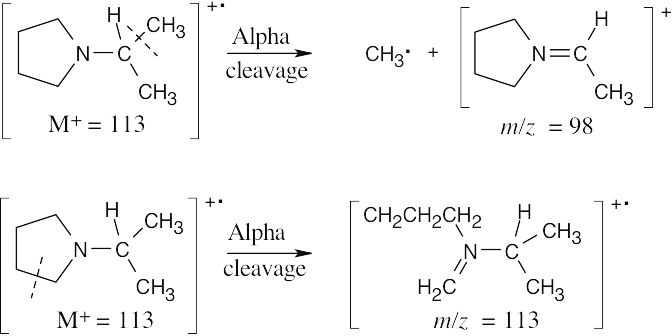
The second product results from cleavage of a bond in the five-membered ring. Due to the symmetry of the amine, only one peak is observed.

Mass Spectrometry

 

 

• (a)The compound contains no more than 7 carbons. As in Problem 12.1, divide the mass to the right of the decimal point by 0.00783 to arrive at an approximate value for the number of hydrogens (10.8). Since the compound has an even mass (and an

 

 

even number of hydrogens), it contains an even number of nitrogens, or no nitrogens. The two most likely formulas are C6H10O (M⁺ = 98.0732) and C5H10N2 (M⁺ = 98.0844). The latter formula agrees precisely with the given molecular ion.

(b)The compound contains no more than 9 carbons, and approximately 4.1 hydrogens. The number of hydrogens must be odd, since M⁺ is odd. Assume the molecule has 5 hydrogens, and adjust the numbers of nitrogens and oxygens until you arrive at the correct value for M⁺. The formula is C6H5NO2.

 

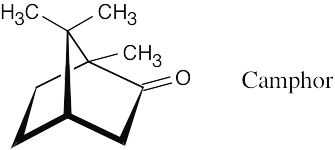
• Reasonable molecular formulas for camphor are C10H16O, C9H12O2, and C8H8O3 (see Problem 12.1). The actual formula, C10H16O (M⁺ = 152.1201), corresponds to three degrees of unsaturation. The ketone functional group accounts for one of these. Since camphor is a saturated compound, the other two degrees of unsaturation are due to two rings.

 

• Carbon is tetravalent, and nitrogen is trivalent. If a C–H unit (formula weight 13) is replaced by an N atom (formula weight 14), the molecular weight of the resulting compound increases by one. Since all neutral hydrocarbons have even-numbered molecular weights (CnH2n+2, CnH2n, and so forth) the resulting nitrogen-containing compounds have odd-numbered molecular weights. If two C–H units are replaced by two N atoms, the molecular weight of the resulting compound increases by two and remains an even number.

 

• Because M⁺ is an odd number, pyridine contains an odd number of nitrogen atoms. If pyridine contained one nitrogen atom (atomic weight 14) the remaining atoms would have a formula weight of 65, corresponding to –C5H5. C5H5N is, in fact, the molecular formula of pyridine.

 

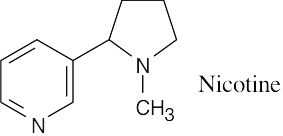
• Subtract the isotopic mass of the two nitrogens from the value of M⁺, and divide the quantity to the right of the decimal point by 0.00783 to find the approximate number of hydrogens in nicotine. The molecular formula of nicotine is C10H14N2. To find the equivalent hydrocarbon formula, subtract the number of nitrogens from the number of hydrogens. The equivalent hydrocarbon formula of nicotine, C10H12, indicates five degrees of unsaturation — two of them due to the two rings and the other three due to three double bonds.

 

 

• Use the technique described in Problem 12.1 to find the molecular formula of cortisone. Cortisone contains approximately 25 hydrogens. Make a table of possible molecular formulas for cortisone that have around 25 hydrogens and calculate the exact molecular weights corresponding to these formulas.

 

Isotopic mass

 

Molecular formula	Mass of carbons	Mass of hydrogens	Mass of oxygens	Mass of molecular ion
C27H20O	324.0000 u	20.1565 u	15.9949 u	360.1514 u
C25H28O2	300.0000	28.2191	31.9898	360.2089
C24H24O3	288.0000	24.1878	47.9847	360.1725
C21H28O5	252.0000	28.2191	79.9746	360.1937

 

The molecular weight of C21H28O5 corresponds to the observed molecular weight of cortisone. (Note that only the last formula has the correct degree of unsaturation, 8).

 

• In order to simplify this problem, neglect the ¹³C and ²H isotopes in determining the molecular ions of these compounds.
• The formula weight of –CH3 is 15, and the atomic masses of the two bromine isotopes are 79 and 81. The two molecular ions of bromoethane occur at M⁺ = 94 (50.7%) and M⁺ = 96 (49.3%).
• The formula weight of –C6H13 is 85, and the atomic masses of the two chlorine isotopes are 35 and 37. The two molecular ions of 1-chlorohexane occur at M⁺ = 120 (75.8%) and M⁺ = 122 (24.2%).

 

• Each carbon atom has a 1.10% probability of being ¹³C and a 98.90% probability of being ¹²C. The ratio of the height of the ¹³C peak to the height of the ¹²C peak for a one- carbon compound is (1.10/98.9) × 100% = 1.11%. For a six-carbon compound, the contribution to (M+1)⁺ from ¹³C is 6 × (1.10/98.9) × 100% = 6.66%. For benzene, the relative height of (M+1)⁺ is 6.66% of the height of M⁺.

A similar line of reasoning can be used to calculate the contribution to (M+1)⁺ from ²H. The natural abundance of ²H is 0.015%, so the ratio of a ²H peak to a ¹H peak for a one- hydrogen compound is 0.015%. For a six-hydrogen compound, the contribution to (M+1)⁺ from ²H is 6 x 0.015% = 0.09%.

For benzene, (M+1)⁺ is 6.75% of M⁺. Notice that ²H contributes very little to the size of (M+1)⁺.

 

 

• (a) The molecular formula of the ketone is C5H10O, and the fragments correspond to the products of alpha cleavage (McLafferty rearrangement fragments have even- numbered values of m/z). Draw all possible ketone structures, show the charged products of alpha cleavage, and note which fragments correspond to those listed.

 

 

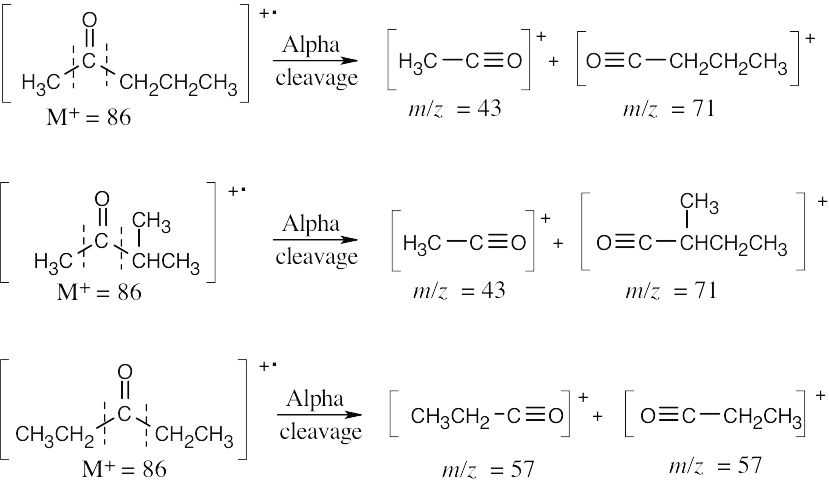
Either of the first two compounds shows the observed fragments in its mass spectrum.

• C5H12O is the formula of an alcohol with M⁺ = 88. The fragment at m/z = 70 is due to the product of dehydration of M⁺. The other two fragments are a result of alpha cleavage. Draw the possible C5 alcohol isomers, and draw their products of alpha cleavage. The tertiary alcohol shown fits the data.

 

 

 

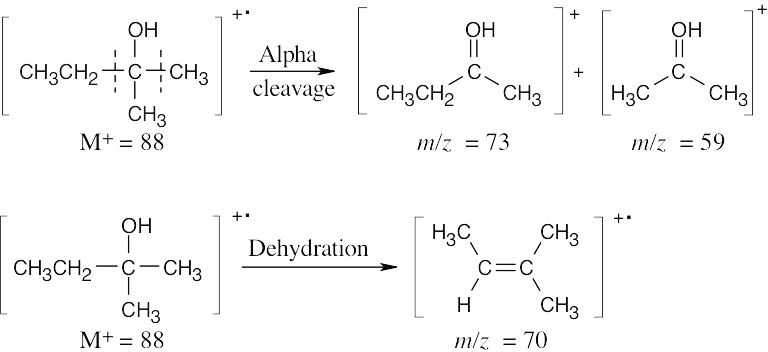
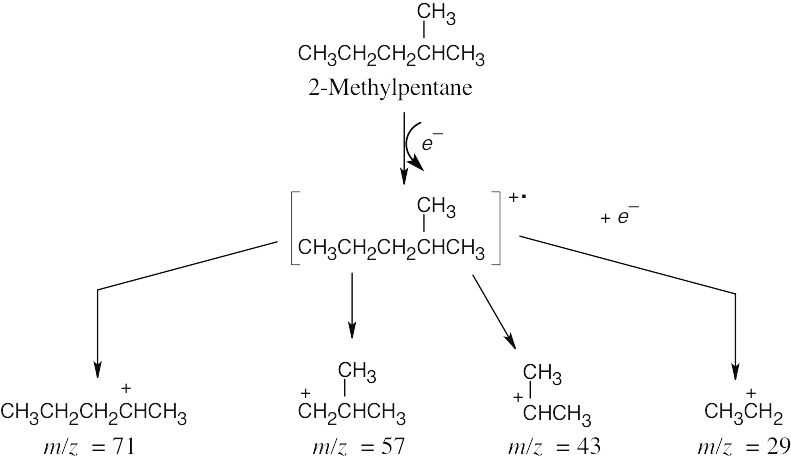
The molecular ion, at m/z = 86, is present in very low abundance. The base peak, at m/z = 43, represents a stable secondary carbocation.

 

• Before doing the hydrogenation, familiarize yourself with the mass spectra of cyclohexene and cyclohexane. Note that M⁺ is different for each compound. After the reaction is underway, inject a sample from the reaction mixture into the mass spectrometer. If the reaction is finished, the mass spectrum of the reaction mixture should be superimposable with the mass spectrum of cyclohexane.

 

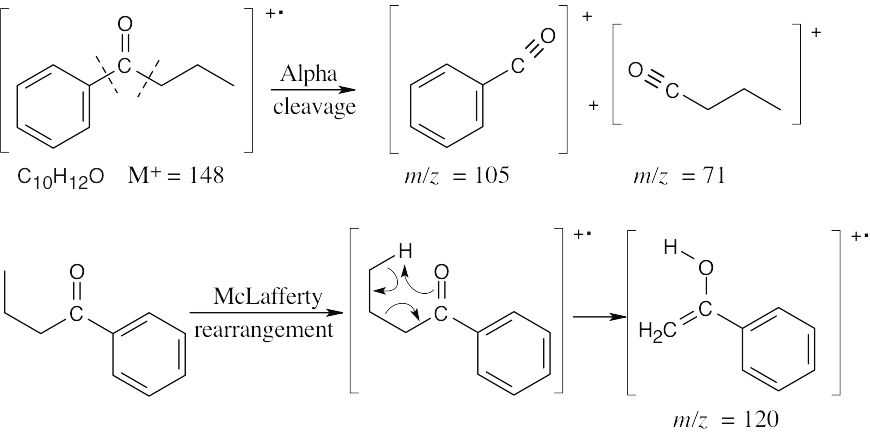
• (a)This ketone shows mass spectrum fragments that are due to alpha cleavage and to the McLafferty rearrangement. The molecular ion occurs at M⁺ = 148, and major fragments have m/z = 120, 105, and 71. (Note that only charged species are shown.)

 

 

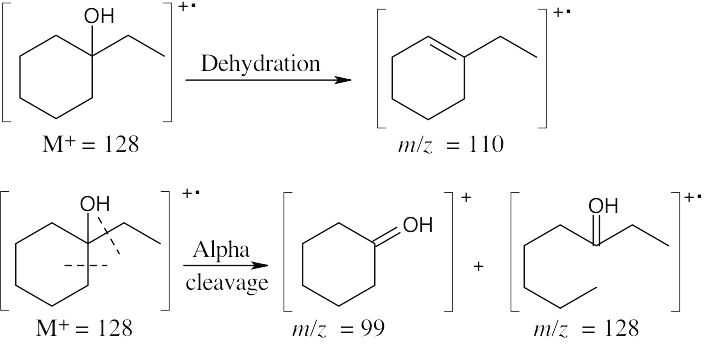
• The fragments in the mass spectrum of this alcohol (C8H16O) result from dehydration and alpha cleavage. Major fragments have m/z values of 128 (the same value as the molecular ion), 110, and 99.

 

 

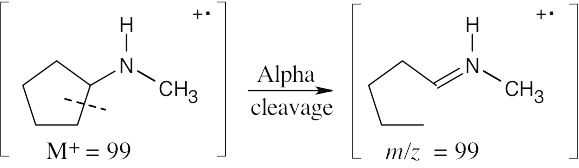
• Amines fragment by alpha cleavage. In this problem, cleavage occurs in the ring, producing a fragment with the same value of m/z as the molecular ion (99).

 

Infrared Spectroscopy

 

• CH3CH2C≡CH shows absorptions at 2100–2260 cm^–1 (C≡C) and at 3300 cm^–1 (C≡C– H) that are due to the terminal alkyne bond.

H2C=CHCH=CH2 has absorptions in the regions 1640–1680 cm^–1 and 3020–3100 that are due to the double bonds. It also shows absorptions at 910 cm^–1 and 990 cm^–1 that are due to monosubstituted alkene bonds. No absorptions occur in the alkyne region.

CH3C≡CCH3. For reasons we will not discuss, symmetrically substituted alkynes such as 2-butyne do not show a C≡C bond absorption in the IR. This alkyne is distinguished from the other isomers in that it shows no absorptions in either the alkyne or alkene regions.

 

• Two enantiomers have identical physical properties (other than the sign of specific rotation). Thus, their IR spectra are also identical.

 

• Since diastereomers have different physical properties and chemical behavior, their IR spectra are also different.

 

 

• (a)Absorptions at 3300 cm^–1 and 2150 cm^–1 are due to a terminal triple bond. Possible structures:

 

CH3CH2CH2C≡CH(CH3)2CHC≡CH

 

• An IR absorption at 3400 cm^–1 is due to a hydroxyl group. Since no double bond absorption is present, the compound must be a cyclic alcohol.

 

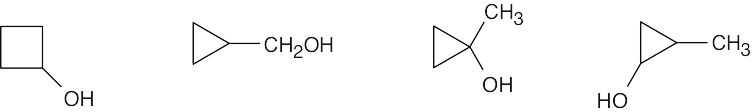
• An absorption at 1715 cm^–1 is due to a ketone. The only possible structure is CH3CH2COCH3.
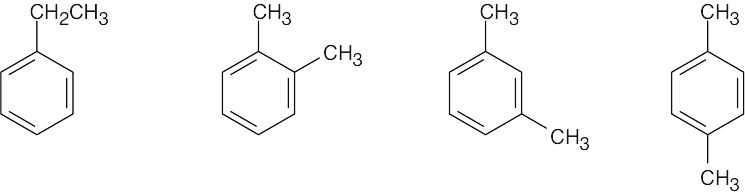
• Absorptions at 1600 cm^–1 and 1500 cm^–1 are due to an aromatic ring. Possible structures:

 

 

12.31
(a)	HC≡CCH2NH2	CH3CH2C≡N
	Alkyne absorptions at 3300 cm–1, 2100–2260 cm–1 Amine absorption at 3300–3500 cm–1	Nitrile absorption at 2210– 2260 cm–1
(b)	CH3COCH3 Strong ketone absorption at 1715 cm–1	CH3CH2CHO Strong aldehyde absorption at 1730 cm–1

 

• Spectrum (b) differs from spectrum (a) in several respects. Note in particular the absorptions at 715 cm^–1 (strong), 1140 cm^–1 (strong), 1650 cm^–1 (medium), and 3000 cm^–1 (medium) in spectrum (b). The absorptions at 1650 cm^–1 (C=C stretch) and 3000 cm^–1 (=C–H stretch) can be found in Table 12.1. They allow us to assign spectrum (b) to cyclohexene and spectrum (a) to cyclohexane.

 

 

• Only absorptions with medium to strong intensity are listed.

 

 

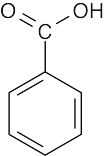• aromatic ring C=C 1450–1600 cm^–1

aromatic ring C–H 3030 cm^–1

carboxylic acid C=O 1710–1760 cm^–1

carboxylic acid O–H 2500–3100 cm^–1

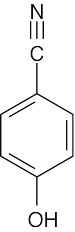(c)aromatic ring C=C 1450–1600 cm^–1

aromatic ring C–H 3030 cm^–1

alcohol O–H 3400–3650 cm^–1

nitrile C≡N

2210–2260 cm^–1

 

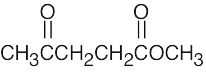(e)ester

1735 cm^–1

• 
  aromatic ring C=C 1450–1600 cm^–1 aromatic ring C–H

3030 cm^–1

aromatic ester 1715 cm^–1

 

 

• alkene C=C

1640–1680 cm^–1

alkene =C–H 3020–3100 cm^–1

ketone

1715 cm^–1

 

 

ketone

1715 cm^–1

 

 

 

 

• (a)CH3C≡CCH3 exhibits no terminal ≡C–H stretching vibration at 3300 cm^–1, as CH3CH2C≡CH does.
• CH3COCH=CHCH3, a ketone next to a double bond, shows a strong ketone absorption at 1690 cm^–1; CH3COCH2CH=CH2 shows a ketone absorption at 1715 cm^–1 and monosubstituted alkene absorptions at 910 cm^–1 and 990 cm^–1.
• CH3CH2CHO exhibits an aldehyde band at 1730 cm^–1; H2C=CHOCH3 shows characteristic monosubstituted alkene absorptions at 910 cm^–1 and 990 cm^–1.

 

• 

	Compound	Distinguishing Absorption	Due to:
(a)		1715 cm–1	C=O (ketone)
(b)	(CH3)2CHCH2C≡CH	2100–2260 cm–1 3300 cm–1	C≡C C≡C–H
(c)	(CH3)2CHCH2CH=CH2	910 cm–1, 990 cm–1 1640–1680 cm–1 3020–3100 cm–1	RCH=CH2 C=C =C–H

 

 

 

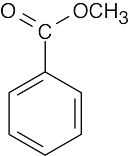
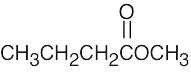• 1735 cm^–1C=O (ester)

 

 

 

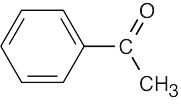(e)1690 cm^–1

 

1450–1600 cm^–1

3030 cm^–1

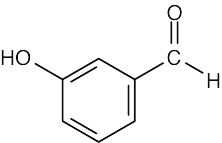(f)1710 cm^–1

 

3400–3650 cm^–1

1450–1600 cm^–1

3030 cm^–1

ketone next to aromatic ring

aromatic ring aromatic ring

 

aldehyde next to aromatic ring

alcohol aromatic ring aromatic ring

 

 

 

 

• 

 

 

 

The infrared spectrum of the starting alcohol shows a broad absorption at 3400–3640 cm^–1 due to an O–H stretch. The alkene product exhibits medium intensity absorbances at 1645–1670 cm^–1 and at 3000–3100 cm^–1. Monitoring the disappearance of the alcohol absorption makes it possible to decide when reaction is complete. It is also possible to monitor the appearance of the alkene absorptions.

 

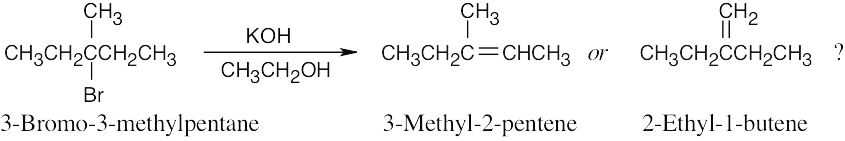
The IR spectra of both products show the characteristic absorptions of alkenes in the regions 3020–3100 cm^–1 and 1650 cm^–1. However, in the region 700–1000 cm^–1, 2- ethyl-1-butene shows a strong absorption at 890 cm^–1 that is typical of 2,2-disubstituted R2C=CH2 alkenes. The presence or absence of this peak should help to identify the product. (3-Methyl-2-pentene is the major product of the dehydrobromination reaction.)

 

 

General Problems

 

• The following expressions are needed:

ɛ = hv = hc/λ = hcṽ, where ṽ is the wavenumber. The last expression shows that, as ṽ increases, the energy needed to cause IR absorption increases, indicating greater bond strength. Thus an ester C=O bond (ṽ =1735 cm⁻¹ ) is stronger than a ketone C=O bond (ṽ = 1715 cm⁻¹).

 

• Possible molecular formulas containing carbon, hydrogen, and oxygen and having M⁺ = 150 are C10H14O, C9H10O2, and C8H6O3. The first formula has four degrees of unsaturation, the second has five degrees of unsaturation, and the third has six degrees of unsaturation. Since carvone has three double bonds (including the ketone) and one ring, or four degrees of unsaturation, C10H14O is the correct molecular formula for carvone.

 

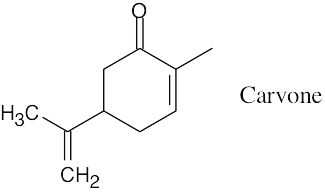
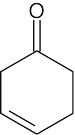
• The intense absorption at 1690 cm^–1 is due to a ketone next to a double bond.

 

• The peak of maximum intensity (base peak) in the mass spectrum occurs at m/z = 67. This peak does not represent the molecular ion, however, because M⁺ of a hydrocarbon must be an even number. Careful inspection reveals the molecular ion peak at m/z = 68. M⁺ = 68 corresponds to a hydrocarbon of molecular formula C5H8 with a degree of unsaturation of two.

Fairly intense peaks in the mass spectrum occur at m/z = 67, 53, 40, 39, and 27. The peak at m/z = 67 corresponds to loss of one hydrogen atom, and the peak at m/z = 53 represents loss of a methyl group. The unknown hydrocarbon thus contains a methyl group.

Significant IR absorptions occur at 2130 cm^–1 (–C≡C– stretch) and at 3320 cm^–1 (≡C–H stretch). These bands indicate that the unknown hydrocarbon is a terminal alkyne.

Possible structures for C5H8 are CH3CH2CH2C≡CH and (CH3)2CHC≡CH. [1-Pentyne is correct.]

 

• The molecular ion, M⁺ = 70, corresponds to the molecular formula C5H10. This compound has one double bond or one ring.

The base peak in the mass spectrum occurs at m/z = 55. This peak represents loss of a methyl group from the molecular ion and indicates the presence of a methyl group in the unknown hydrocarbon. All other peaks occur with low intensity.

 

 

In the IR spectrum, it is possible to distinguish absorptions at 1660 cm^–1 and at 3000 cm^–1 due to a double bond. (The 2960 cm^–1 absorption is rather hard to detect because it occurs as a shoulder on the alkane C–H stretch at 2850–2960 cm^–1.) Since no absorptions occur in the region 890 cm^–1–990 cm^–1, we can exclude terminal alkenes as possible structures. The remaining possibilities for C5H10 are CH3CH2CH=CHCH3 and (CH3)2C=CHCH3. [2- Methyl-2-butene is correct.]

 

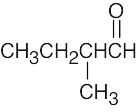
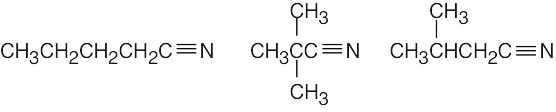• (b)

 

 

 

 

• The simplest way to distinguish between the two isomers is by taking their IR spectra. The aldehyde carbonyl group absorbs at 1730 cm^–1, and the ketone carbonyl group absorbs at 1715 cm^–1.

The mass spectra of the two isomers also differ. Like ketones, aldehydes also undergo alpha cleavage and McLafferty rearrangements.

McLafferty rearrangement:

The fragments from the McLafferty rearrangements differ in values of m/z. Alpha cleavage:

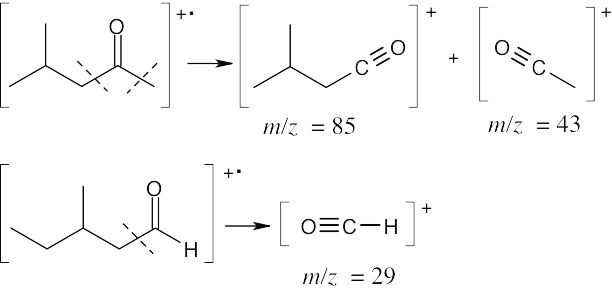
The fragments resulting from alpha cleavage also differ in values of m/z.

 

 

 

The absorption at 3400 cm^–1 is due to a hydroxyl group.

 

• The absorption at 3400^–1 is due to an alcohol.

 

 

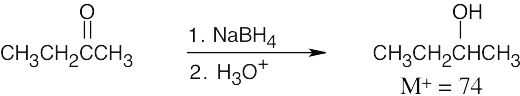
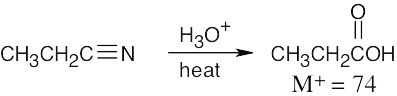
The absorption at 1710 cm^–1 is due to the carbonyl group of a carboxylic acid, and the absorption at 2500–3100 cm^–1 is due to the –OH group of the carboxylic acid.

 

• Ethyl octanoate

O

 

O

 

• 2-Methyl-1-pentene

 

• Chlorobenzene

 

 

 

 

 

 

 

 

This file is copyright 2023, Rice University. All Rights Reserved.