4 Chapter 4 – Organic Compounds: Cycloalkanes and Their Stereochemistry
Chapter 4 – Organic Compounds: Cycloalkanes and Their Stereochemistry
Solutions to Problems
| 4.1 |
The steps for naming a cycloalkane are very similar to the steps used for naming an open- chain alkane. |
| |
Step 1: Name the parent cycloalkane. In (a), the parent is cyclohexane. If the compound has an alkyl substituent with more carbons than the ring size, the compound is named as a cycloalkyl-substituted alkane, as in (c).
Step 2: Identify the substituents. In (a), both substituents are methyl groups.
Step 3: Number the substituents so that the second substituent receives the lowest possible number. In (a), the substituents are in the 1- and 4- positions.
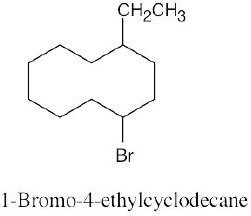
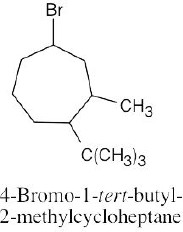
Step 4: Name the compound. If two different alkyl groups are present, cite them alphabetically. Halogen substituents follow the same rules as alkyl substituents.
|
| 4.2 |
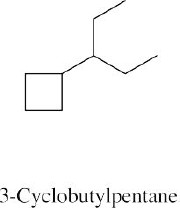
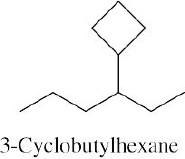
To draw a substituted cycloalkane, simply draw the ring and attach substituents in the specified positions. The structure in (b) is named as a cyclobutyl-substituted alkane because the alkyl chain has more carbons than the ring.
|
| 4.3 |
|
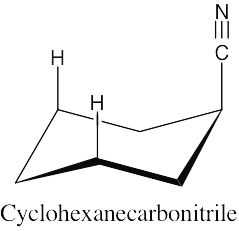
| |
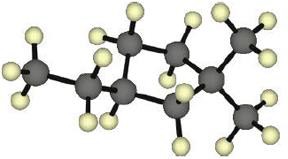 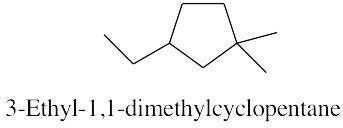 |
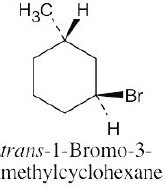
| 4.4 |
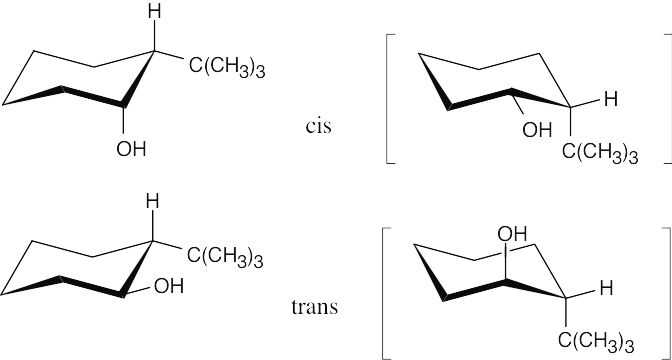
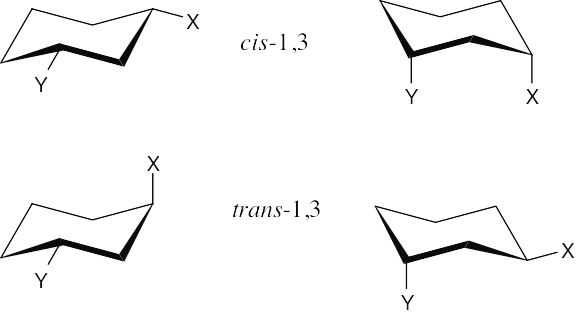
Two substituents are cis if they both have either dashed or wedged bonds. The substituents are trans if one has a wedged bond and the other has a dashed bond.
| (a)
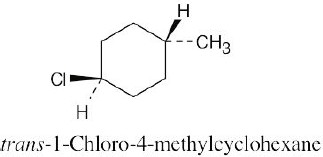
|
(b)
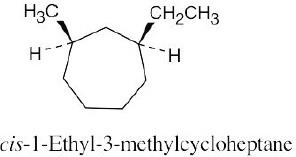
|
|
| 4.6 |
The two hydroxyl groups on the cyclopentyl ring are cis because they both point behind the plane of the page (both dashed bonds). The carbon chains have a trans relationship (one is dashed and the other is wedged). |
| 4.7 |
| (a)
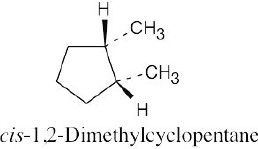
|
(b)
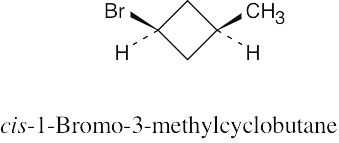
|
|
| 4.8 |
All hydrogen atoms on the same side of the cyclopropane ring are eclipsed by neighboring hydrogens. If we draw each hydrogen–hydrogen interaction, we count six eclipsing interactions, three on each side of the ring. Since each of these interactions costs 4.0 kJ/mol, all six cost 24.0 kJ/mol. 24 kJ/mol ÷115 kJ/mol × 100% = 21% of the total strain energy of cyclopropane is due to torsional strain. |
| 4.9 |
The added energy cost of eclipsing interactions causes cis-1,2-dimethylcyclopropane to be of higher energy and to be less stable than the trans isomer. |
| 4.10 |
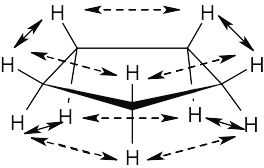
If cyclopentane were planar, it would have ten hydrogen–hydrogen interactions with a total energy cost of 40 kJ/mol (10 × 4.0 kJ/mol). The measured total strain energy of 26 kJ/mol indicates that 14 kJ/mol of eclipsing strain in cyclopentane (35%) has been relieved by puckering. |
| 4.11 |
| (a)
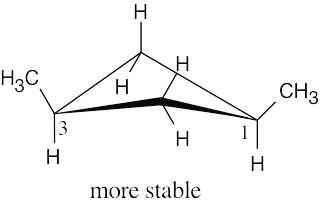
|
(b)
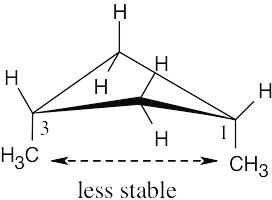
|
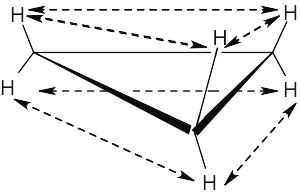
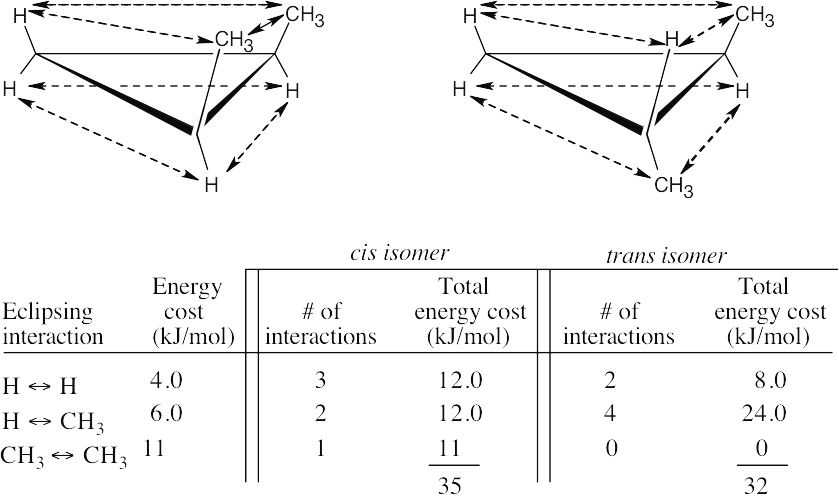
The methyl groups are farther apart in the more stable conformation of cis-1,3- dimethylcyclobutane. |
| 4.12 |
Use the technique in Section 4.5 to draw the cyclohexane ring. Figure 4.11 shows how to attach axial (a) and equatorial (e) bonds.
The conformation with –OH in the equatorial position is more stable.
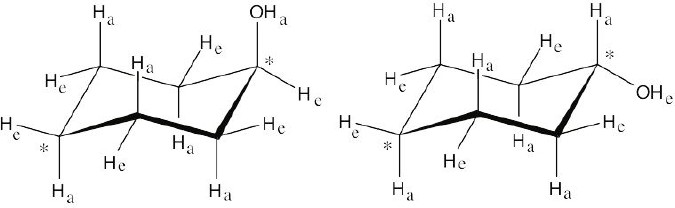
Note: The starred ring carbons lie in the plane of the paper. |
| 4.13 |
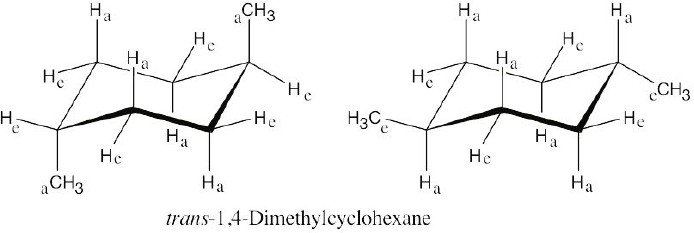
In trans-1,4-disubstituted cyclohexanes, the methyl substituents are either both axial or both equatorial.
|
| 4.14 |
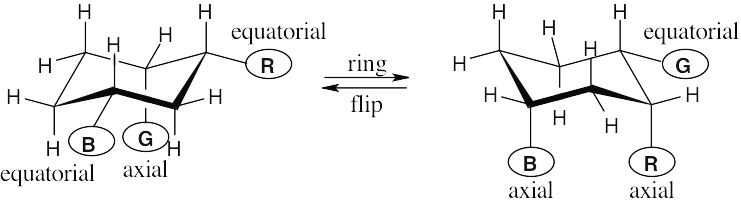
In a ring-flip, an axial substituent becomes equatorial, and an equatorial substituent becomes axial.
|
| 4.15 |
Table 4.1 shows that an axial hydroxyl group causes 2 × 2.1 kJ/mol of steric strain. Thus, the energy difference between axial and equatorial cyclohexanol is 4.2 kJ/mol.
|
| 4.16 |
There is very little energy difference between an axial and an equatorial cyano group because the small linear cyano group takes up very little room and produces practically no 1,3-diaxial interactions.
|
| 4.17 |
Table 4.1 shows that an axial bromine causes 2 × 1.0 kJ/mol of steric strain. Thus, the energy difference between axial and equatorial bromocyclohexane is 2.0 kJ/mol. According to Figure 4.13, this energy difference corresponds approximately to a 75:25 ratio of more stable:less stable conformer. Thus, 75% of bromocyclohexane molecules are in the equatorial conformation, and 25% are in the axial conformation at any given moment. |
| 4.18 |
Draw the two chair conformations of each molecule, and look for gauche and 1,3-diaxial interactions. Use Table 4.1 to estimate the values of the interactions. Calculate the total strain; the conformation with the smaller value for strain energy is more stable.
| (a)
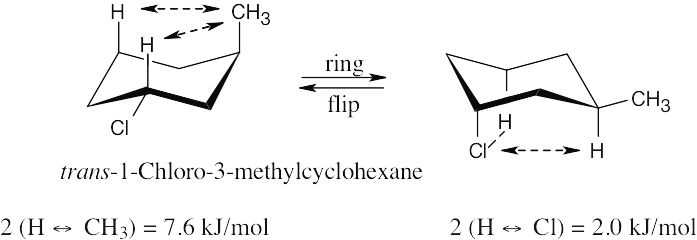
The second conformation is more stable than the first. |
| (b)
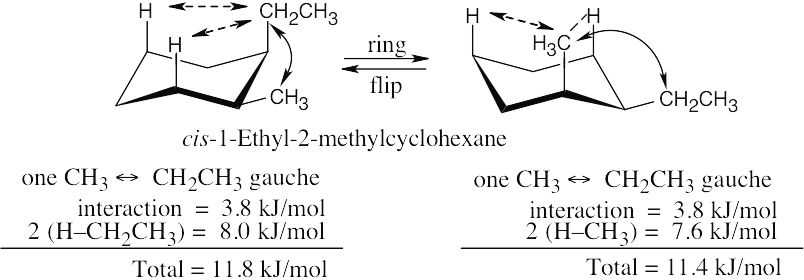
The second conformation is slightly more stable than the first. |
| (c)
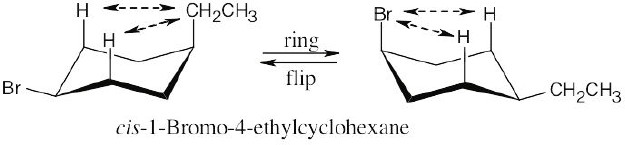
2 (H ↔ CH2CH3) = 8.0 kJ/mol. 2 (H ↔ Br) = 2.0 kJ/mol
The second conformation is more stable than the first. |
| (d)
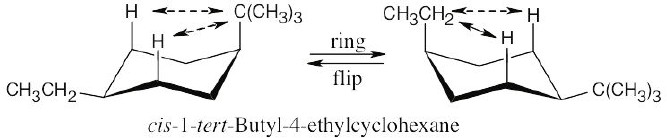
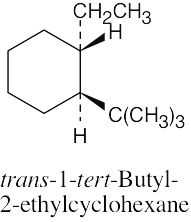
2 [H ↔ C(CH3)3] = 22.8 kJ/mol 2(H ↔ CH2CH3) = 8.0 kJ/mol
The second conformation is more stable than the first. |
|
| 4.19 |
The three substituents have the orientations shown in the first structure. To decide if the conformation shown is the more stable conformation or the less stable conformation, perform a ring-flip on the illustrated conformation and do a calculation of the total strain in each structure as in the previous problem. Notice that each conformation has a Cl – CH3 gauche interaction, but we don’t need to know its energy cost because it is present in both conformations.
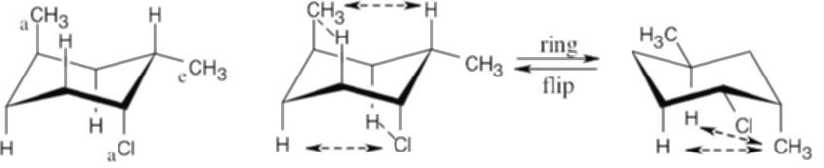
2 [H ↔ CH3] = 7.6 kJ/mol 2 [H ↔ CH3] = 7.6 kJ/mol
2 [H ↔ Cl]= 2.0 kJ/mol
= 9.6 kJ/mol
|
The illustrated conformation is the less stable chair form. |
| 4.20 |
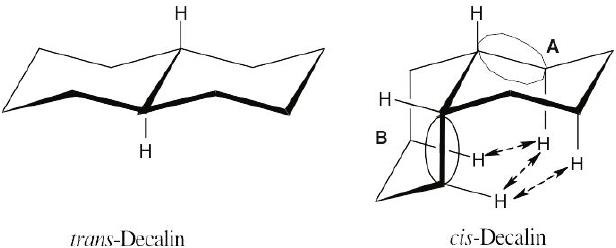
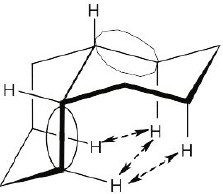
Trans-decalin is more stable than cis-decalin because of three 1,3-diaxial interactions present in the cis isomer. You can recognize these interactions if you think of the circled parts of cis-decalin as similar to axial methyl groups. The gauche interactions that occur with axial methyl groups also occur in cis-decalin. |
| 4.21 |
Both ring fusions are trans because the bridgehead groups are on opposite faces of the fused ring system. |
Additional Problems
Visualizing Chemistry
| 4.22 |
| (a)
|
(b)
|
|
| 4.23 |
|
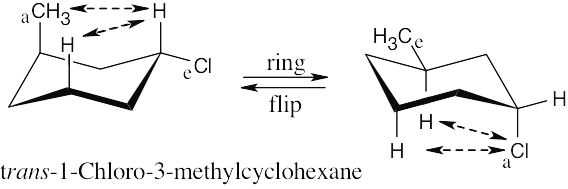 2 (H ↔CH3) = 7.6 kJ/mol 2 (H ↔Cl) = 2.0 kJ/mol 2 (H ↔CH3) = 7.6 kJ/mol 2 (H ↔Cl) = 2.0 kJ/mol
|
The conformation shown (the left structure) is the less stable conformation. |
| 4.25 |
The green substituent is axial, and the red and blue substituents are equatorial.
|
| 4.26 |
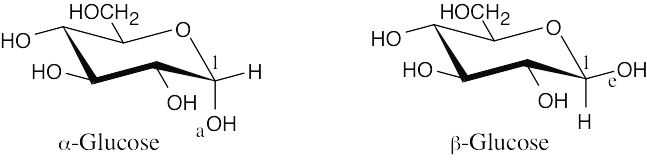
The only difference between α-glucose and β-glucose is in the orientation of the –OH group at carbon 1: the –OH group is axial in α-glucose, and it is equatorial in β-glucose. You would expect β-glucose to be more stable because all of its substituents are in the equatorial position. |
| 4.28 |
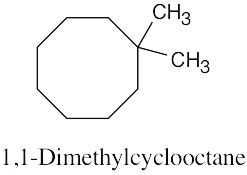
| (a) methylcycloheptane |
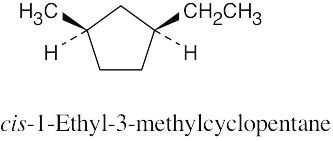
| (b) cis-1,3-dimethylcyclopentane |
| (c) trans-1,2-dimethylcyclohexane |
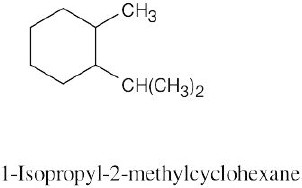
| (d) trans-1-isopropyl-2-methylcyclobutane |
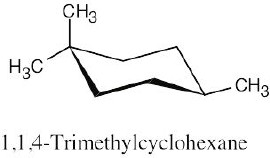
| (e) 1,1,4-trimethylcycloheaxane |
|
| 4.29 |
Stereoisomers have different three-dimensional geometry.
|
| 4.31 |
Stereoisomers:

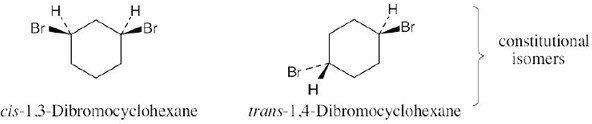
Constitutional isomers of trans-1,2-dichlorocyclobutane: |

trans-1,3-Dichlorocyclobutane is also a constitutional isomer. |
|
| 4.33 |
Two cis–trans isomers of 1,3,5-trimethylcyclohexane are possible. In one isomer (A), all methyl groups are cis; in B, one methyl group is trans to the other two. |
Cycloalkane Conformation and Stability
| 4.35 |
Make a model of cis-1,2-dichlorocyclohexane. Notice that all cis substituents are on the same side of the ring and that two adjacent cis substituents have an axial–equatorial relationship. Now, perform a ring-flip on the cyclohexane.
After the ring-flip, the relationship of the two substituents is still axial–equatorial. No two adjacent cis substituents can be converted to being both axial or both equatorial by a ring- flip. Don’t forget that there are only two chair conformations of any given cyclohexane. |
| 4.36 |
For a trans-1,2-disubstituted cyclohexane, two adjacent substituents must be either both axial or both equatorial.
A ring flip converts two adjacent axial substituents to equatorial substituents, and vice versa. As in Problem 4.35, no two adjacent trans substituents can have an axial-equatorial relationship. |
| 4.37 |
A cis-1,3-disubstituted isomer exists almost exclusively in the diequatorial conformation, which has no 1,3-diaxial interactions. The trans isomer must have one group axial, leading to 1,3-diaxial interactions. Thus, the trans isomer is less stable than the cis isomer. When a molecule has two conformations available, the molecule exists mainly in the lower energy conformation. |
| 4.38 |
The trans-1,4-isomer is more stable because both substituents can be equatorial. |
| 4.39 |
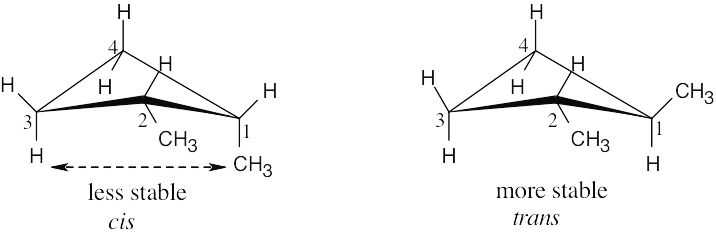
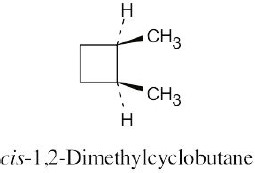
Two types of interactions are present in cis-1,2-dimethylcyclobutane. One interaction occurs between the two methyl groups, which are almost eclipsed. The other is an across- the-ring interaction between methyl groups at position 1 of the ring and a hydrogen at Position 3. Because neither of these interactions are present in trans isomer, it is more stable than the cis isomer. |
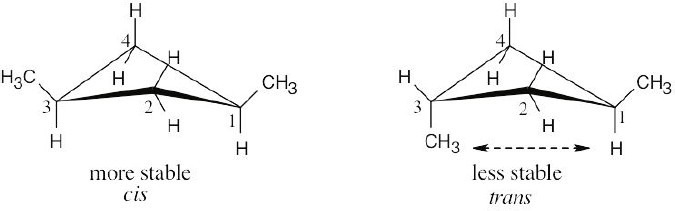
In trans-1,3-dimethylcyclobutane, an across-the-ring interaction occurs between the methyl group at position 3 of the ring and a hydrogen at position 1. Because no interactions are present in the cis isomer, it is more stable than the trans isomer. |
|
| 4.40 |
To solve this problem:
(1) Find the energy cost of a 1,3-diaxial interaction by using Table 4.1.
(2) Convert this energy difference into a percent by using Figure 4.13.
|
| 4.41 |
Make sure you know the difference between axial–equatorial and cis–trans. Axial substituents are parallel to the axis of the ring; equatorial substituents lie around the equator of the ring. Cis substituents are on the same side of the ring; trans substituents are on opposite sides of the ring.
| (a)
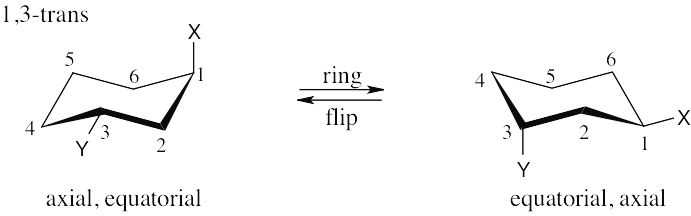
|
| (b)
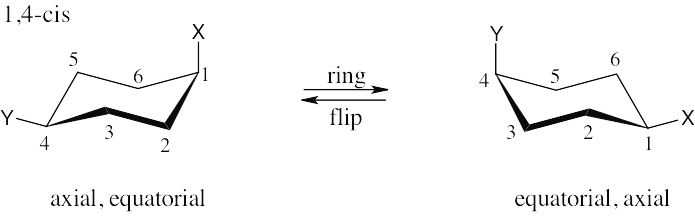
|
| (c)
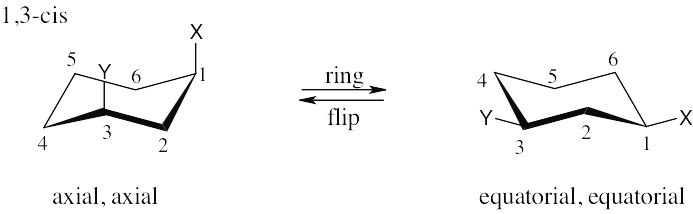
|
| (d) 1,5-trans is the same as 1,3-trans. |
| (e) 1,5-cis is the same as 1,3-cis. |
| (f)

1,6-trans is the same as 1,2-trans. |
|
Cyclohexane Conformational Analysis
| 4.42 |
Use Table 4.1 to find the values of 1,3-diaxial interactions. For the first conformation, the steric strain is 2 × 1.0 kJ/mol = 2.0 kJ/mol. The steric strain in the second conformation is 2 × 3.8 kJ/mol, or 7.6 kJ/mol. The first conformation is more stable than the second conformation by 5.6 kJ/mol. |
| 4.43 |
Use Table 4.1 to find the values of 1,3-diaxial interactions. The first conformation is more stable than the second conformation by a maximum of 9.6 kJ/mol. (A gauche interaction between the two substituents in the diequatorial conformation reduces the value of the energy difference, but its value can’t be determined with the given data.) |
| 4.44 |
In this conformation, all substituents, except for one hydroxyl group, are equatorial. |
| 4.45 |
From the flat-ring drawing you can see that the methyl group and the –OH group have a cis relationship, and the isopropyl group has a trans relationship to both of these groups. Draw a chair cyclohexane ring and attach the groups with the correct relationship.
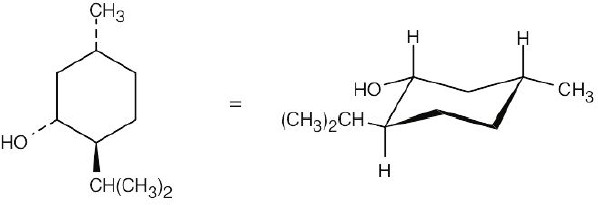 In this conformation, all substituents are equatorial. Now, perform a ring flip. In this conformation, all substituents are equatorial. Now, perform a ring flip. |
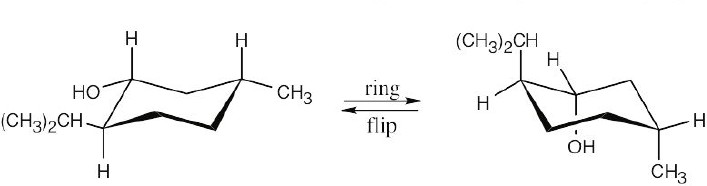 The second conformation is less stable because all substituents are axial. The second conformation is less stable because all substituents are axial. |
|
| 4.46 |
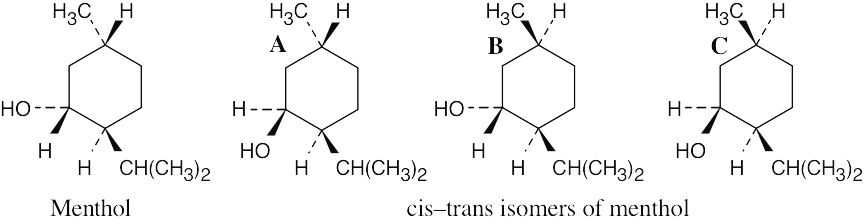
The substituents on the ring have the following relationships:
|
Menthol |
Isomer A |
Isomer B |
Isomer C |
| –CH(CH3)2, –CH3 |
trans |
trans |
cis |
cis |
| –CH(CH3)2, –OH |
trans |
cis |
trans |
cis |
| –CH3, –OH |
cis |
trans |
trans |
cis |
|
|
| 4.47 |
The large energy difference between conformations is due to the severe 1,3 diaxial interaction between the two methyl groups. |
| 4.48 |
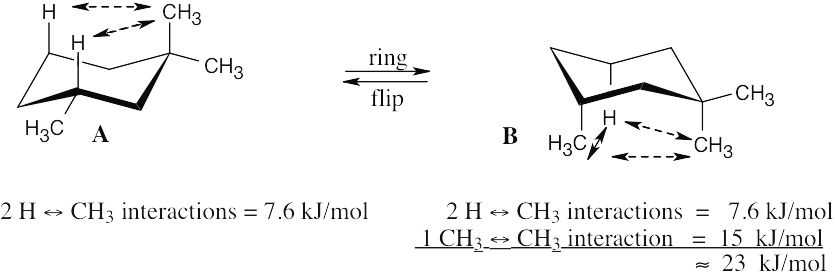
Diaxial cis-1,3-dimethylcyclohexane contains three 1,3-diaxial interactions – two H ↔ CH3 interactions of 3.8 kJ/mol each, and one CH3 ↔ CH3 interaction. If the diaxial conformation is 23 kJ/mol less stable than the diequatorial, 23 kJ/mol – 2(3.8 kJ/mol) ≈ 15 kJ/mol of this strain energy must be due to the CH3 ↔ CH3 interaction. |
| 4.49 |
Conformation A is favored. |
| 4.50 |
Conformation A of cis-1-chloro-3-methylcyclohexane has no 1,3-diaxial interactions and is the more stable conformation. Steric strain in B is due to one CH3 ↔ H interaction (3.8 kJ/mol), one Cl ↔ H interaction (1.0 kJ/mol) and one CH3 ↔ Cl interaction. Since the total-strain energy of B is 15.5 kJ/mol, 15.5 kJ/mol – 3.8 kJ/mol – 1.0 kJ/mol = 10.7 kJ/mol of strain is caused by a CH3 ↔ Cl interaction. |
General Problems
| 4.51 |
Note: In working with decalins, it is essential to use models. Many structural features of decalins that are obvious with models are not easily visualized with drawings.
No 1,3-diaxial interactions are present in trans-decalin.
At the ring junction of cis-decalin, one ring acts as an axial substituent of the other (see circled bonds). The circled part of ring B has two 1,3-diaxial interactions with ring A (indicated by arrows). Similarly, the circled part of ring A has two 1,3-diaxial interactions with ring B; one of these interactions is the same as an interaction of part of the B ring with ring A. These three 1,3-diaxial interactions have a total energy cost of 3 × 3.8 kJ/ mol = 11.4 kJ/mol. Cis-decalin is therefore less stable than trans-decalin by 11.4 kJ/mol. |
| 4.52 |
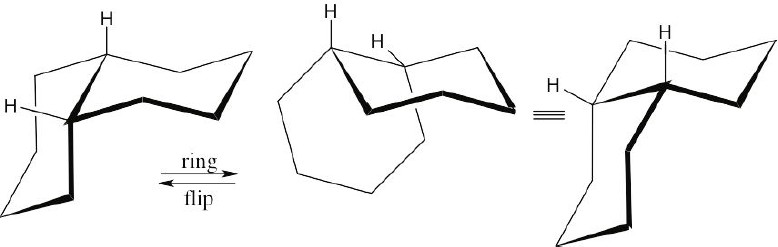
A ring-flip converts an axial substituent into an equatorial substituent and vice versa. At the ring junction of trans-decalin, each ring is a trans–trans diequatorial substituent of the other. If a ring-flip were to occur, the two rings would become axial substituents of each other. You can see with models that a diaxial ring junction is impossibly strained. Consequently, trans-decalin does not ring-flip.
The rings of cis-decalin are joined by an axial bond and an equatorial bond. After a ring- flip, the rings are still linked by an equatorial and an axial bond. No additional strain or interaction is introduced by a ring-flip of cis-decalin.
|
| 4.53 |
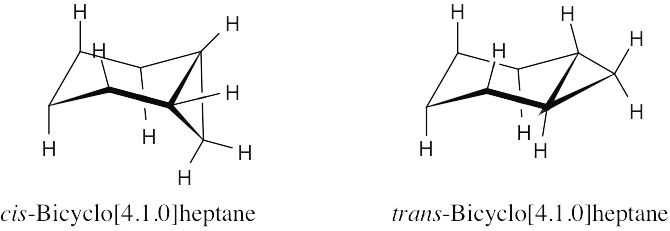
Build models to see the stability difference between the two [4.1.0] ring systems. In both cases, fusing a three-membered ring to a six-membered ring distorts the bond angles of both rings, causing angle strain. This strain is much more severe in the trans isomer than in the cis isomer.
|
| 4.54 |
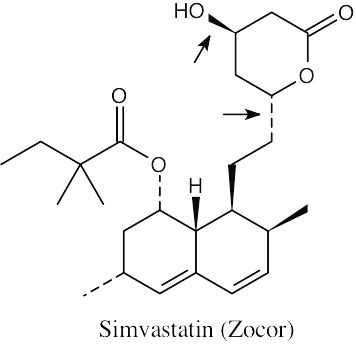
(a) The indicated bonds on simvastatin are trans.
(b) The –H bond and the –OH bond have a cis relationship. The third bond is trans to both of them.
(c) The three indicated bonds on atorvastatin are attached to sp2-hybridized carbons of a planar ring and lie in the same plane. |
| 4.55 |
In the flat-ring structure shown, all –OH groups have an alternating relationship except for the starred group (below). If all of the groups had a trans relationship, the most stable conformation would have all –OH groups in the equatorial position. We expect that the most stable conformation of this structure has one group in the axial position.
Draw both rings and add –OH groups having the indicated relationships. Perform a ring- flip on the structure you have drawn to arrive at the other conformation.
|
| 4.56 |
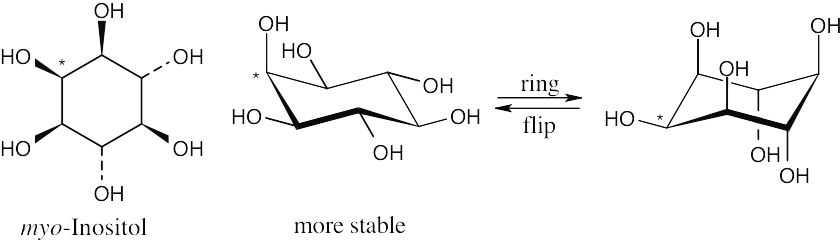
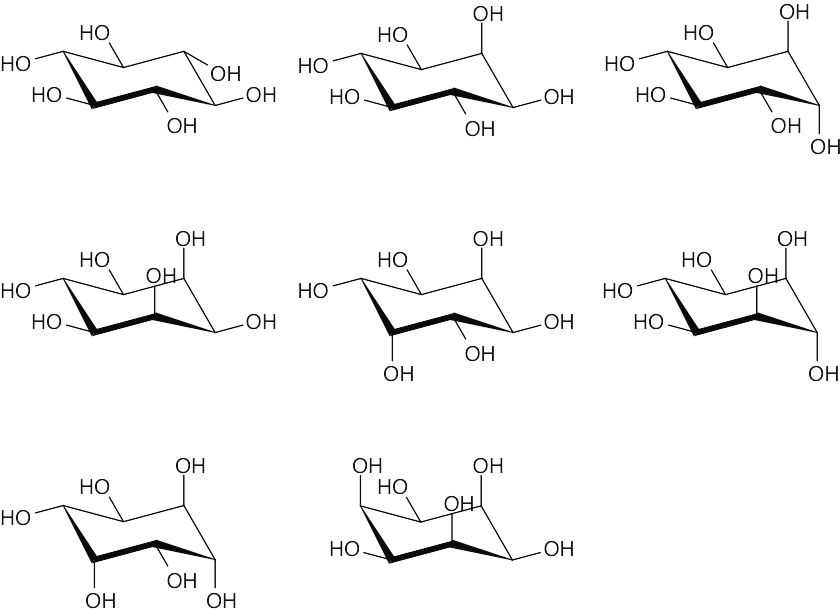
There are eight cis–trans stereoisomers of myo-inositol. The first isomer is the most stable because all hydroxyl groups can assume an equatorial conformation. |
| 4.57 |
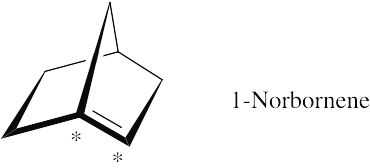
If you build a model of 1-norbornene, you will find that it is almost impossible to form the bridgehead double bond. sp2-Hybridization at the double bond requires all carbons bonded to the starred carbons to lie in a common plane in order for the p orbitals to overlap to form the π bond. The bicyclic ring system forces these atoms out of plane, and the bridgehead double bond can’t form. |
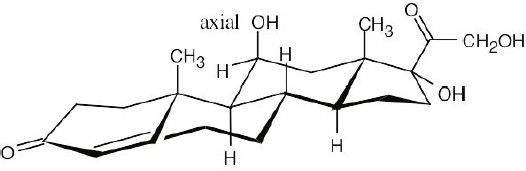
| 4.58 |
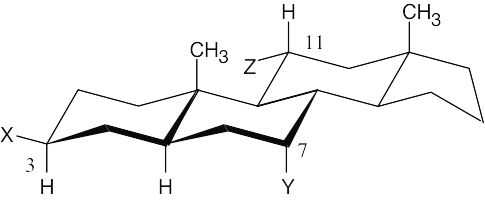
A steroid ring system is fused, and ring-flips don’t occur. Thus, substituents such as the methyl groups shown remain axial. Substituents on the same side of the ring system as the methyl groups are in alternating axial and equatorial positions. Thus, an “up” substituent at C3 (a) is equatorial.
Substituents on the bottom side of the ring system also alternate axial and equatorial positions. A substituent at C7 (b) is axial, and one at C11 (c) is equatorial
|
| 4.60 |
The two trans-1,2-dimethylcyclopentanes are mirror images. |
| 4.61 |
Draw the four possible isomers of 4-tert-butylcyclohexane-1,3-diol. Make models of these isomers also. The bulky tert-butyl group determines the stable conformation because of its strong preference for the equatorial position.
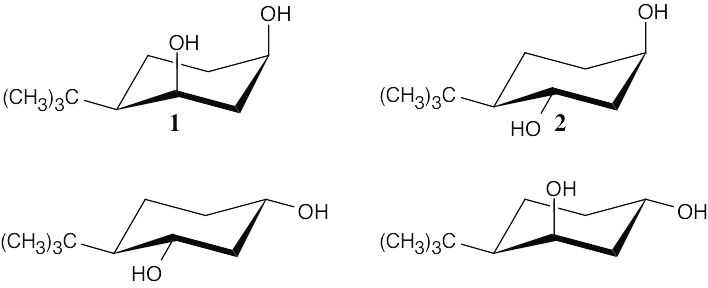
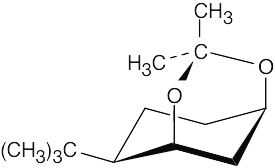
Only when the two hydroxyl groups are cis diaxial (structure 1) can the ketal ring form. In any other conformation, the oxygen atoms are too far apart to be incorporated into a six- membered ring.
|
|
| 4.62 |
All four conformations of the two isomers are illustrated. The second conformation of each pair has a high degree of steric strain, and thus each isomer adopts the first conformation. Since only the cis isomer has the hydroxyl group in the necessary axial position, it oxidizes faster than the trans isomer. |
This file is copyright 2023, Rice University. All Rights Reserved.






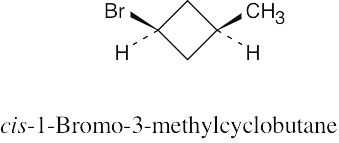


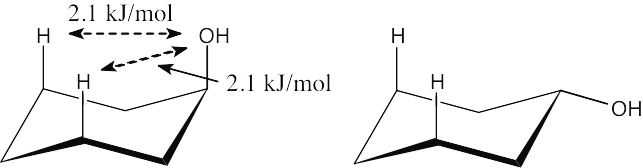

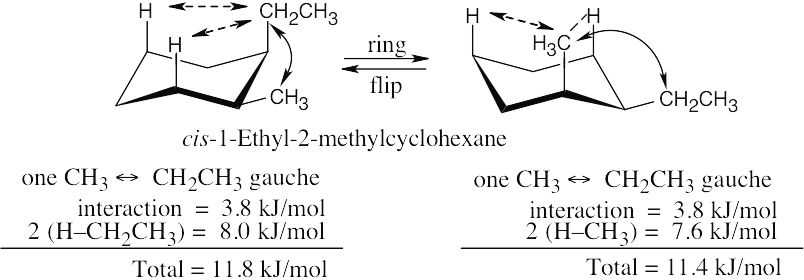





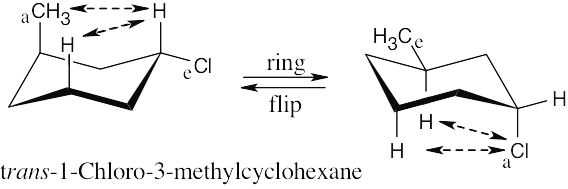 2 (H ↔CH3) = 7.6 kJ/mol 2 (H ↔Cl) = 2.0 kJ/mol
2 (H ↔CH3) = 7.6 kJ/mol 2 (H ↔Cl) = 2.0 kJ/mol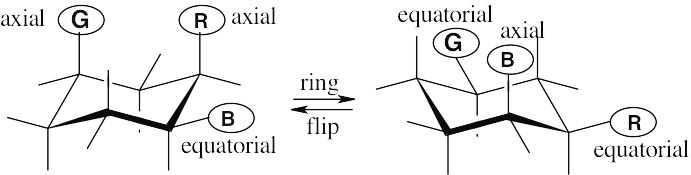







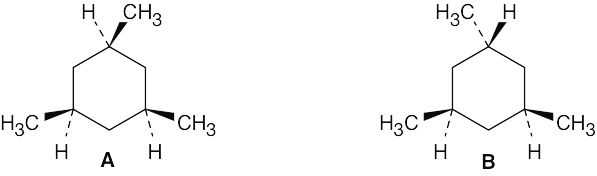
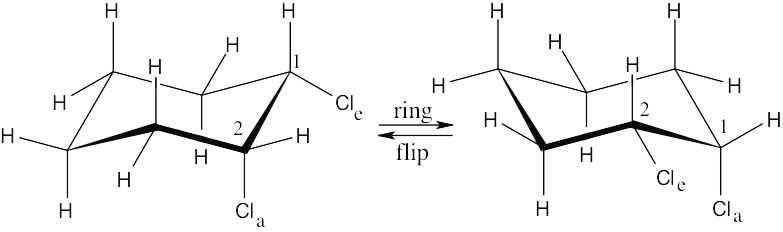
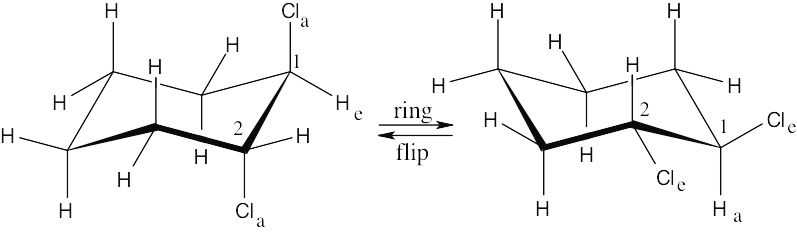
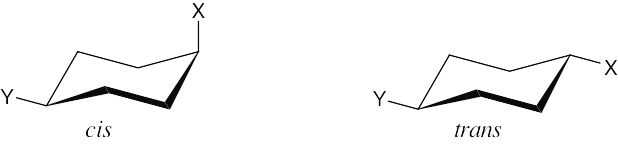









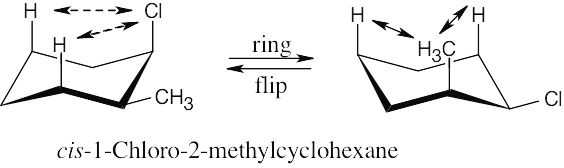
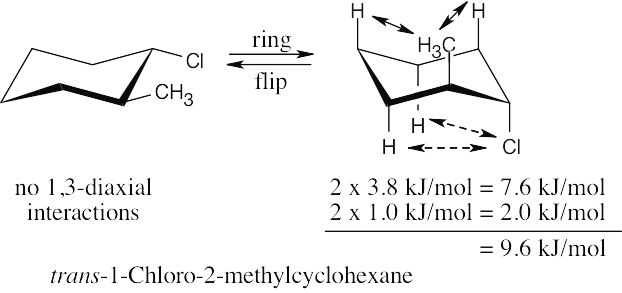
 In this conformation, all substituents are equatorial. Now, perform a ring flip.
In this conformation, all substituents are equatorial. Now, perform a ring flip. The second conformation is less stable because all substituents are axial.
The second conformation is less stable because all substituents are axial.