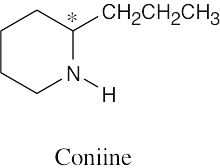
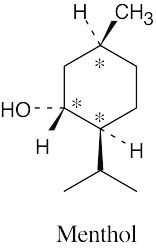
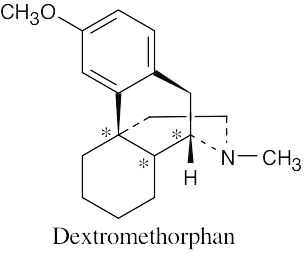
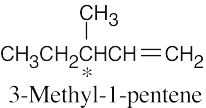
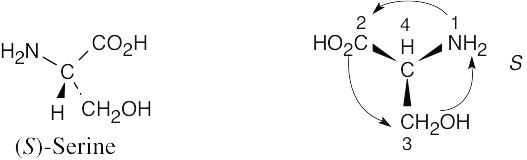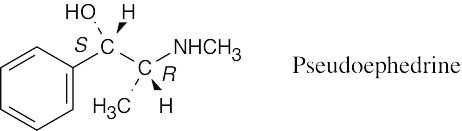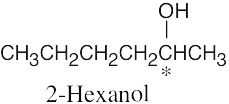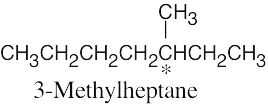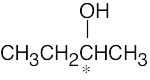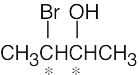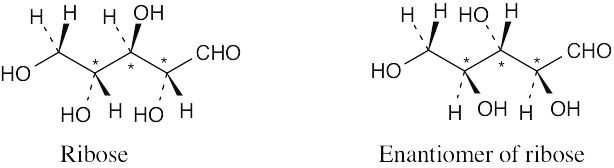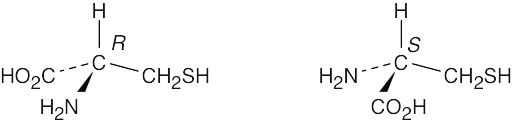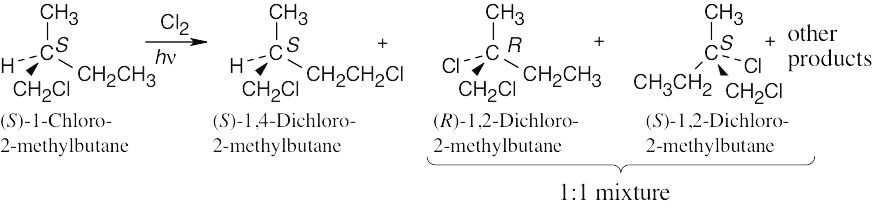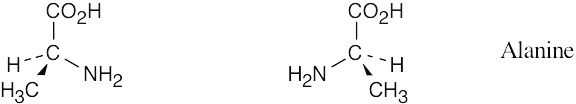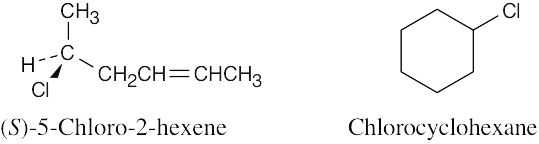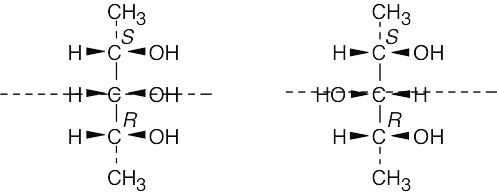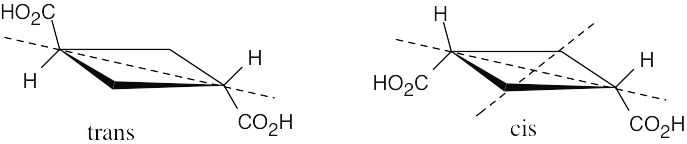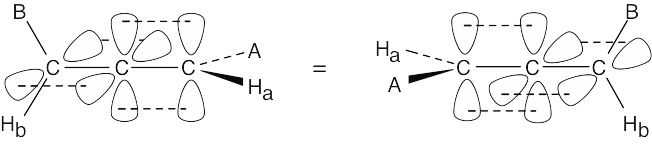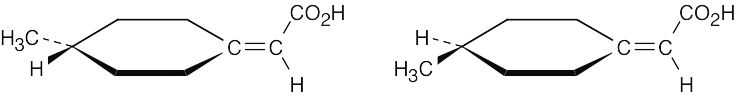5 Chapter 5 – Stereochemistry at Tetrahedral Centers
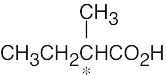
| 5.3 |
Refer to Problem 5.2 if you need help.
|
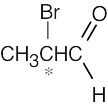
| 5.4 |
(a) |
 |
|
(b) |
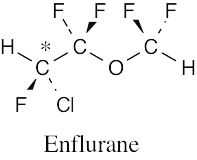 |
| 5.5 |
By convention, a (–) rotation indicates rotation to the left, and thus cocaine is levorotatory. |
| 5.6 |
Use the formula [α ]D |
= |
[latex]\frac{α}{l×C}[/latex], where |
|
[α ]D |
= |
specific rotation |
|
[latex]α[/latex] |
= |
observed rotation |
|
[latex]l[/latex] |
= |
path length of cell (in dm) |
|
[latex]C[/latex] |
= |
concentration (in g/mL) |
|
In this problem, [latex]α[/latex] |
= |
1.21° |
|
[latex]l[/latex] |
= |
5.00 cm = 0.500 dm |
|
[latex]C[/latex] |
= |
1.50 g/10.0 mL = 0.150 g/mL |
|
[α ]D |
= |
[latex]\frac{+1.21°}{0.500 dm× 0.150 g/mL}[/latex] |
| 5.7 |
Review the sequence rules presented in Section 5.5. A summary: |
|
Rule 1: |
An atom with a higher atomic number has priority over an atom with a lower atomic number. |
|
Rule 2: |
If a decision can’t be reached by using Rule 1, look at the second, third, or fourth atom away from the double-bond carbon until a decision can be made. |
|
Rule 3: |
Multiple-bonded atoms are equivalent to the same number of single-bonded atoms. |
|
|
Higher |
Lower |
Rule |
| (a) |
–Br |
–H |
1 |
| (b) |
–Br |
–Cl |
1 |
| (c) |
–CH2CH3 |
–CH3 |
2 |
| (d) |
–OH |
–NH2 |
1 |
| (e) |
–CH2OH |
–CH3 |
2 |
| (f) |
–CH=O |
–CH2OH |
3 |
|
| 5.8 |
Use the sequence rules in Section 5.5. |
|
(a) |
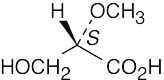
By Rule 1, –H is of lowest priority, and –OH is of highest priority. By Rule 2, –CH2CH2OH is of higher priority than –CH2CH3.
Highest → Lowest
–OH, –CH2CH2OH, –CH2CH3, –H |
|
(b) |
By Rule 3, –CO2H is considered as . Because 3 oxygens are attached to a –CO2H carbon and only one oxygen is attached to –CH2OH, –CO2H is of higher priority than -CH2OH. –CO2CH3 is of higher priority than –CO2H by Rule 2, and –OH is of highest priority by Rule 1. . Because 3 oxygens are attached to a –CO2H carbon and only one oxygen is attached to –CH2OH, –CO2H is of higher priority than -CH2OH. –CO2CH3 is of higher priority than –CO2H by Rule 2, and –OH is of highest priority by Rule 1.
Highest → Lowest |
|
(b) |
–OH, –CO2CH3, –CO2H, –CH2OH |
|
(c) |
–NH2, –CN, –CH2NHCH3, –CH2NH2 |
|
(d) |
–SSCH3, –SH, –CH2SCH3, –CH3 |
| 5.9 |
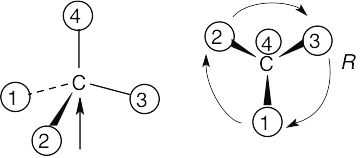
All stereochemistry problems are easier if you use models. Part (a) will be solved by two methods – with models and without models. |
|
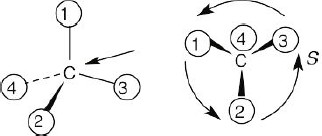
(a) |
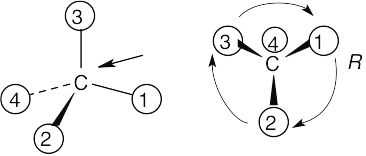
With models: Build a model of (a). Orient the model so that group 4 is pointing to the rear. Note the direction of rotation of arrows that go from group 1 to group 2 to group. The arrows point counterclockwise, and the configuration is S.
Without models: Imagine yourself looking at the molecule, with the group of lowest priority pointing to the back. Your viewpoint would be at the upper right of the molecule, and you would see group 1 on the left, group 3 on the right and group 2 at the bottom. The arrow of rotation travels counterclockwise, and the configuration is S.
|
|
(a) |
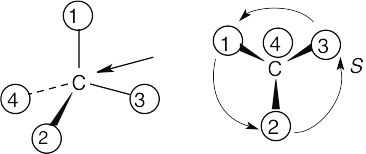 |
|
(b) |
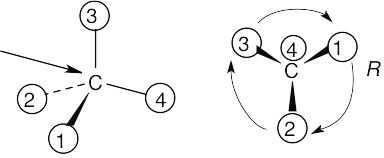 |
|
(c) |
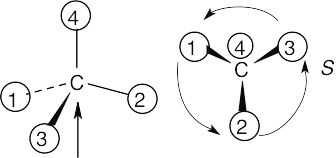 |
| 5.10 |
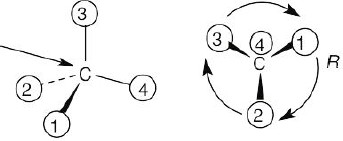
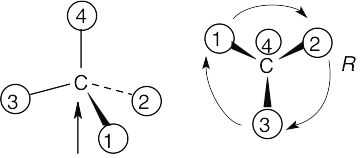
Step 1: |
For each chirality center, rank substituents by the Cahn–Ingold–Prelog system; give the number 4 to the lowest priority substituent. For part (a):
| Substituent |
Priority |
| -SH |
1 |
| -CO2H2 |
2 |
| -CH3 |
3 |
| -H |
4 |
|
|
Step 2: |
As in the previous problem, orient yourself so that you are 180° from the lowest priority group (indicated by the arrow in the drawing). From that viewpoint, draw the molecule as it looks when you face it. Draw the arrow that travels from group 1 to group 2 to group 3, and note its direction of rotation. The molecule in (a) has S configuration. |
|
|
(a) |
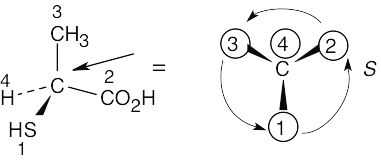 |
|
|
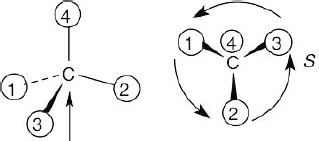
(b) |
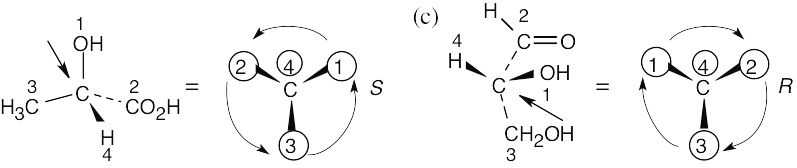
In (b), the observer is behind the page, looking out and down toward the right. In (c), the observer is behind the page looking out and up to the left.
|
| 5.11 |
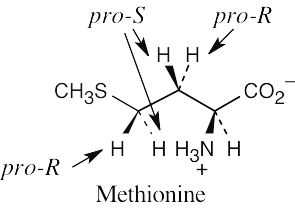
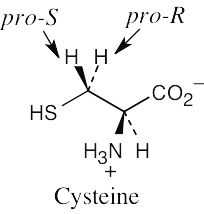
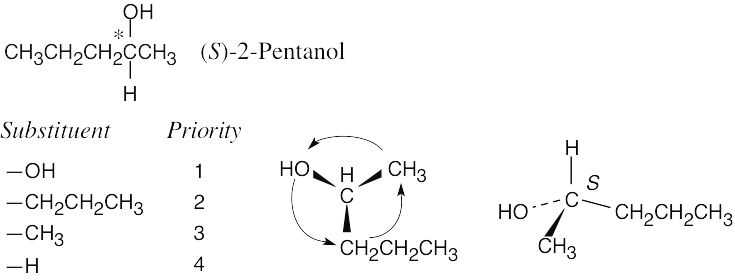 |
| 5.12 |
Fortunately, methionine is shown in the correct orientation.
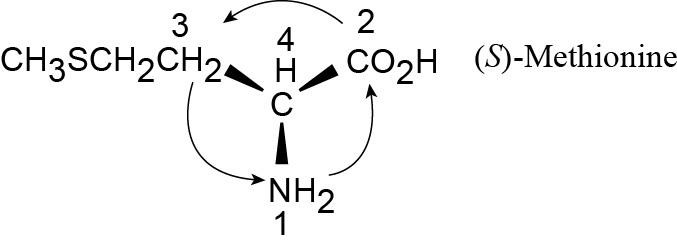
|
| 5.13 |
For (a): (Note: the phosphate group is represented as P.)

(a) R,R (b) S,R (c) R,S (d) S,S
a, d are enantiomers and are diastereomeric with b, c. b, c are enantiomers and are diastereomeric with a, d.
Structure (a) is D-erythrose 4-phosphate, structure (d) is its enantiomer, and structures (b) and (c) are its diastereomers.
|
| 5.14 |
Morphine has five chirality centers and, in principle, can have 25 = 32 stereoisomers. Most of these stereoisomers are too strained to exist.

|
| 5.15 |
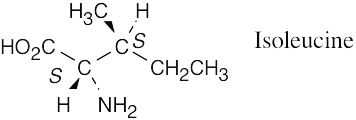 |
| 5.16 |
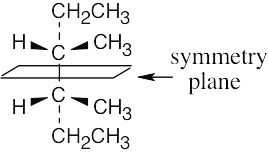
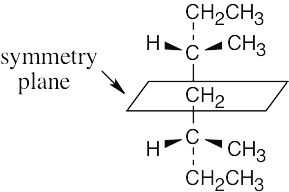
To decide if a structure represents a meso compound, try to locate a plane of symmetry that divides the molecule into two halves that are mirror images. Molecular models are always helpful. |
|
(a) |
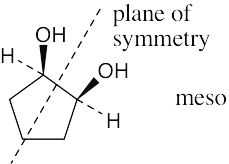 |
|
(b) |
and (c) are not meso structures |
|
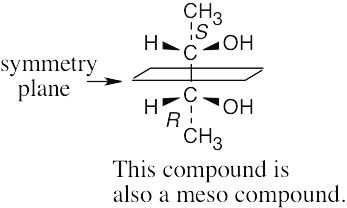
(d) |
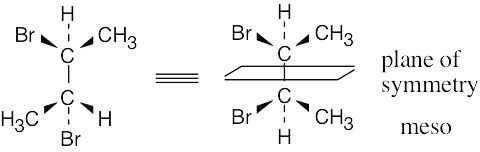 |
| 5.17 |
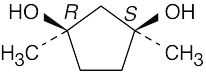
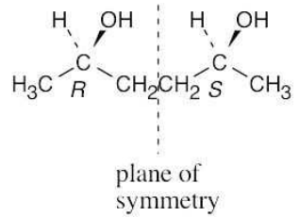
For a molecule to exist as a meso form, it must possess a plane of symmetry. 2,3- Butanediol can exist as a pair of enantiomers or as a meso compound, depending on the configurations at carbons 2 and 3. |
|
(a) |
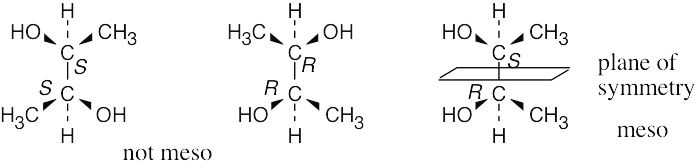 |
|
(b) |
2,3-Pentanediol has no symmetry plane and thus can’t exist in a meso form. |
|
(c) |
2,4-Pentanediol can exist in a meso form.
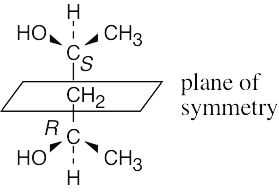
2,4-Pentanediol can also exist as a pair of enantiomers (2R,4R) and (2S,4S) that are not meso compounds.
|
| 5.18 |
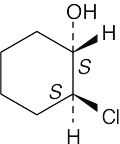
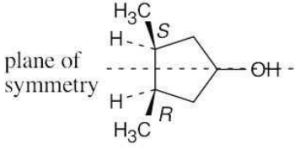
The molecule represents a meso compound. The symmetry plane passes through the carbon bearing the –OH group and between the two ring carbons that are bonded to methyl groups.
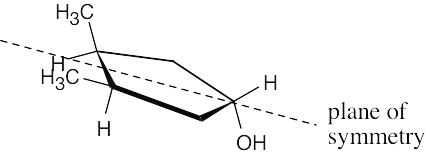
|
| 5.19 |
The product is the pure S-ester. No new chirality centers are formed during the reaction, and the configuration at the chirality center of (S)-2-butanol is unchanged.
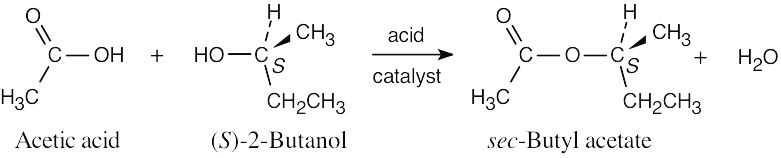
|
| 5.20 |
The two product salts have the configurations (R,S) and (S,S) and are diastereomers.
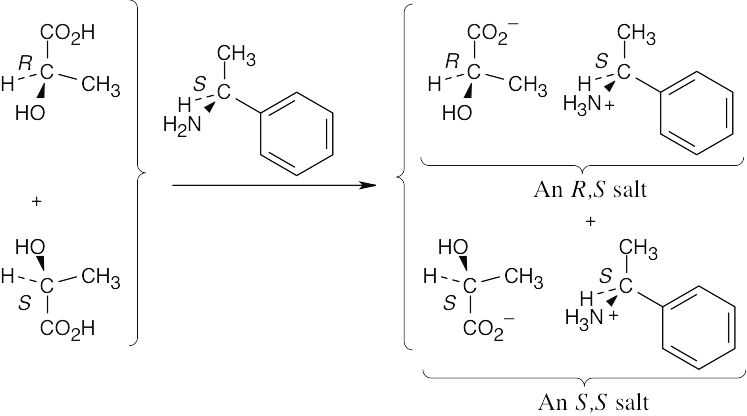
|
| 5.21 |
(a) |
These two compounds are constitutional isomers (skeletal isomers).
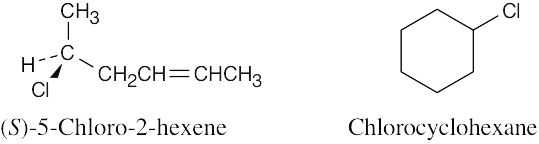
|
|
(b) |
The two dibromopentane stereoisomers are diastereomers. |
| 5.22 |
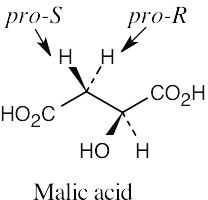
For each molecule, replace the left hydrogen with 2H. Give priorities to the groups and assign R,S configuration to the chirality center. If the configuration is R, the replaced hydrogen is pro-R, and if the configuration is S, the replaced hydrogen is pro-S. |
|
(a) |
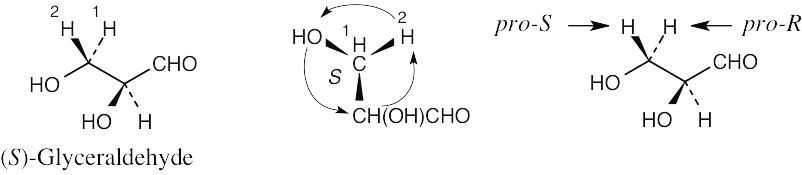 |
|
(b) |
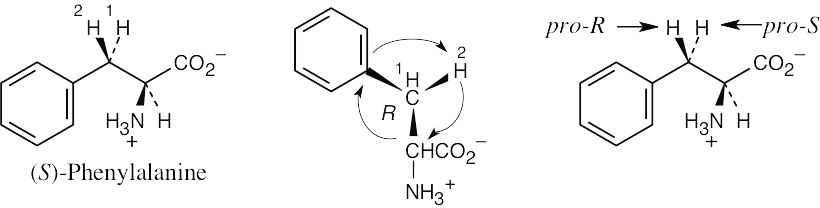 |
| 5.23 |
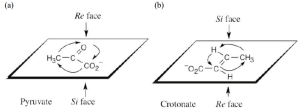
Draw the plane that includes the sp2 carbon and its substituents, and rank the substituents. For the upper face, draw the arrow that proceeds from group 1 to group 2 to group 3. If the direction of rotation is clockwise, the face is the Re face; if rotation is counterclockwise, the face is the Si face. |
|
(a) |
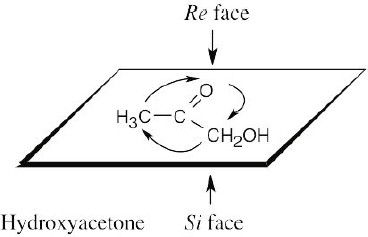 |
|
(b) |
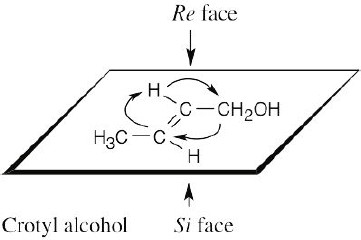 |
| 5.24 |
Use the strategy in the previous problem to identify the faces of the plane that contains the sp2 carbon. Draw the product that results from reaction at the Re face, and assign configuration to the chirality center.
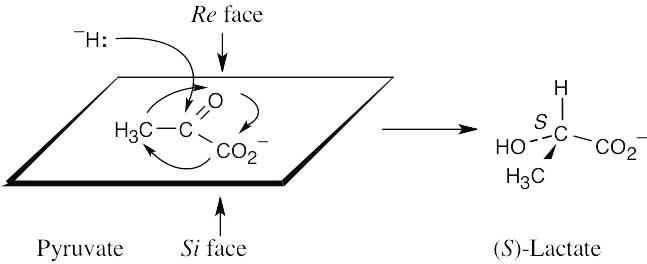
|
| 5.25 |
Addition of –OH takes place on the Re face of C2 of aconitate. Addition of –H occurs on the Re face of C3 to yield (2R,3S)-isocitrate. H and OH add from opposite sides of the double bond.
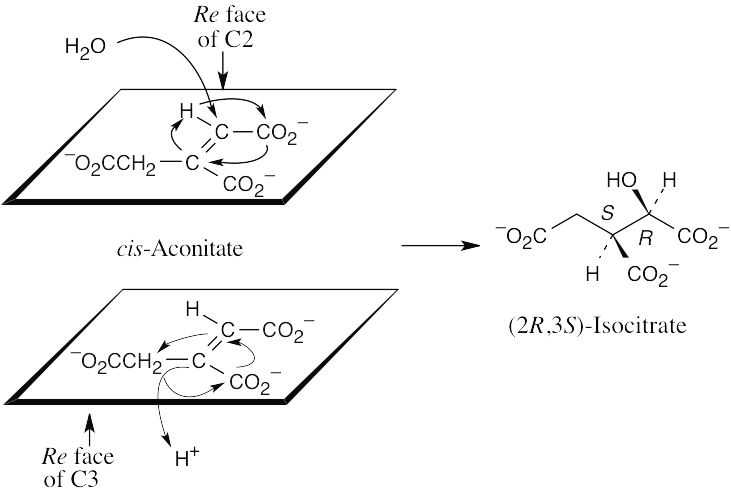
|
Additional Problems
Visualizing Chemistry
| 5.26 |
Structures (a), (b), and (d) are identical (R enantiomer), and (c) represents the S enantiomer. |
| 5.27 |
(a) |
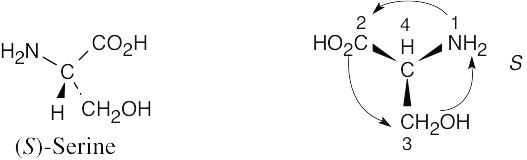 |
|
(b) |
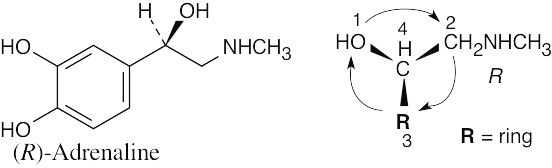 |
| 5.28 |
Locate the plane of symmetry that identifies the structure as a meso compound. |
|
(a) |
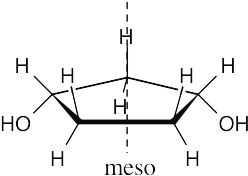 |
|
(b) |
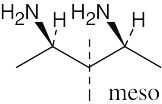 |
|
(c) |
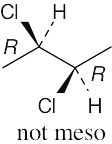 |
| 5.29 |
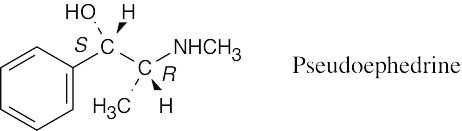 |
Chirality and Optical Activity
| 5.31 |
Chiral: (d) golf club, (e) spiral staircase
Achiral: (a) basketball, (b) fork, (c) wine glass, (f) snowflake
|
| 5.34 |
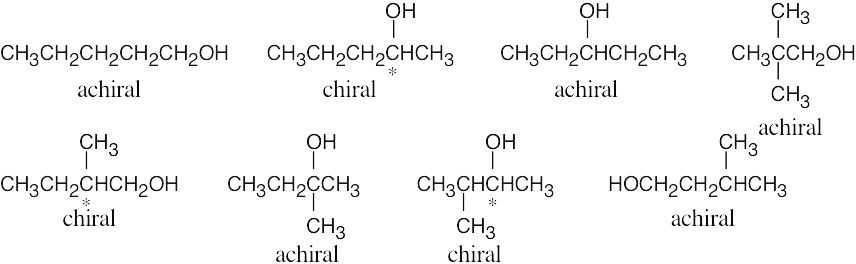
|
| 5.36 |
Erythronolide B has ten chirality centers.
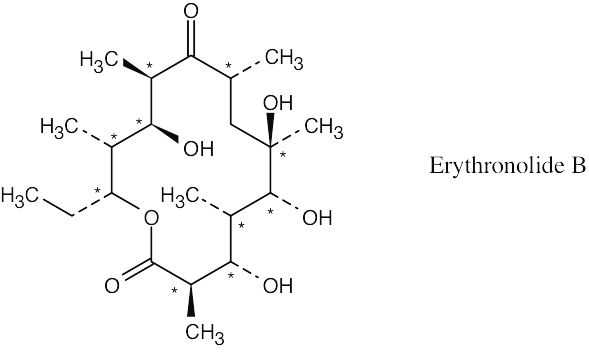
|
Assigning Configuration to Chirality Centers
| 5.37 |
Identical molecules: b (S enantiomer), c (R enantiomer), d (S enantiomer); Pair of enantiomers: a |
| 5.38 |
The specific rotation of (2R,3R)-dichloropentane is equal in magnitude and opposite in sign to the specific rotation of (2S,3S)-dichloropentane because the compounds are enantiomers. There is no predictable relationship between the specific rotations of the (2R,3S) and (2R,3R) isomers because they are diastereomers. |
| 5.39-5.40 |
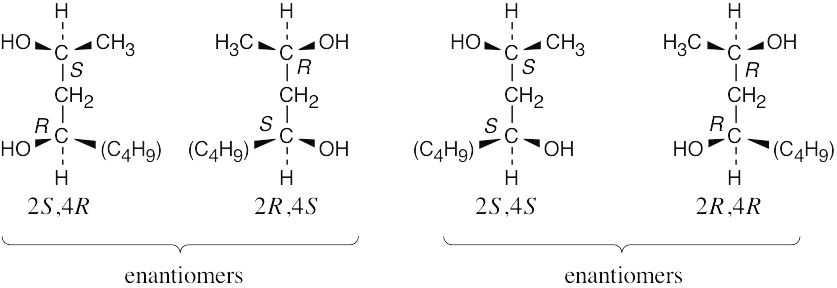
The (2R,4S) stereoisomer is the enantiomer of the (2S,4R) stereoisomer.
The (2S,4S) and (2R,4R) stereoisomers are diastereomers of the (2S,4R) stereoisomer.
|
| 5.42 |
|
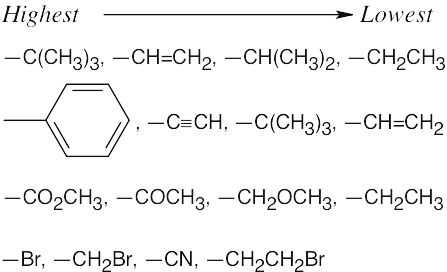
|
|
(a) |
|
(b) |
|
(c) |
|
(d) |
| 5.45 |
(a) |
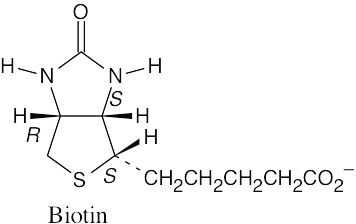 |
|
(b) |
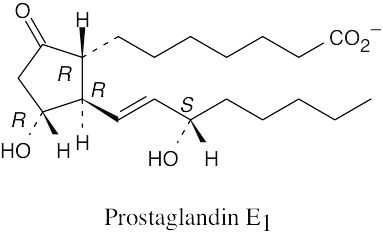 |
| 5.46 |
(a) |
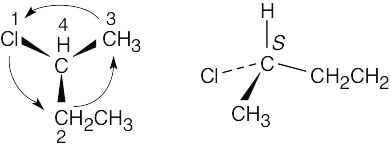 |
|
(b) |
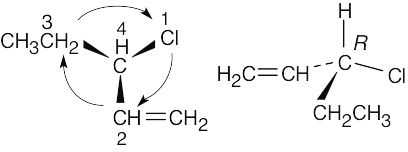 |
| 5.47 |
(a) |
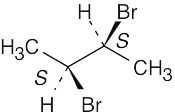 |
|
(b) |
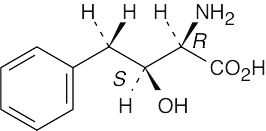 |
| 5.48 |
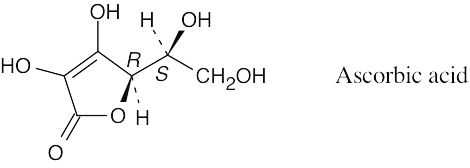 |
| 5.49 |
(a) |
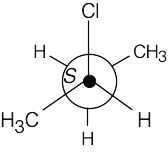 |
|
(b) |
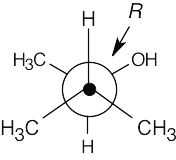 |
| 5.50 |
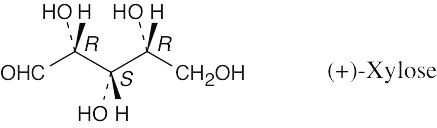 |
Meso Compounds
| 5.53 |
Both of the diastereomers shown below are meso compounds with three chirality centers. Each is a meso compound because it has a symmetry plane, and in each structure the central carbon is bonded to four different groups (a group with R configuration, a group with S configuration, –OH, and –H).
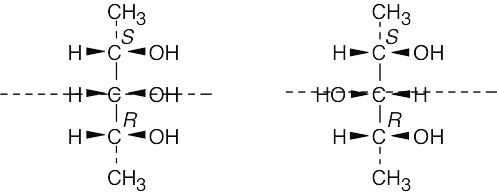
|
| 5.54 |
(a)-(c) |
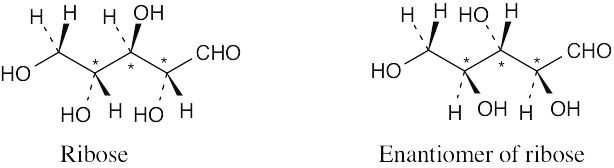
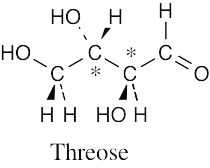
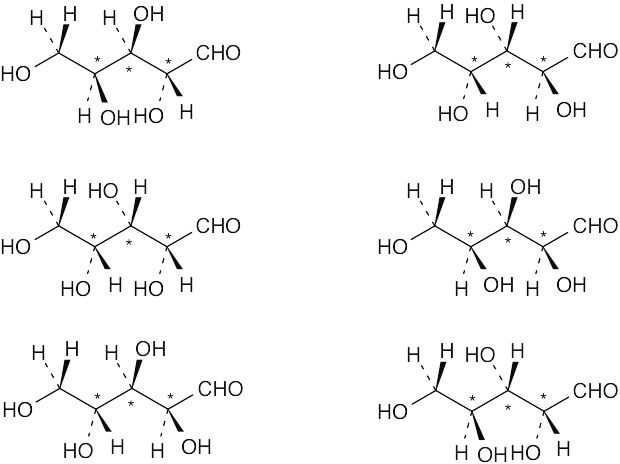
Ribose has three chirality centers, which give rise to eight (23) stereoisomers. |
|
(d) |
Ribose has six diastereomers.
|
| 5.55 |
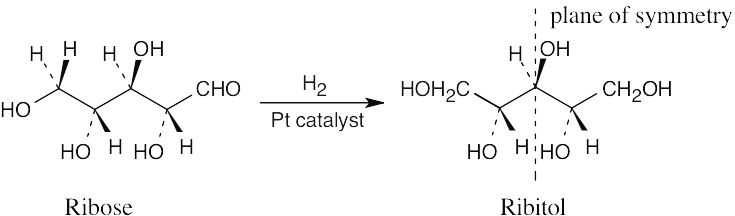
Ribitol is an optically inactive meso compound. Catalytic hydrogenation converts the aldehyde functional group into a hydroxyl group and makes the two halves of ribitol mirror images of each other.
|
Prochirality 5.56
| 5.57 |
 |
| 5.58 |
Remember that each sp2 carbon has a Re face and a Si face.
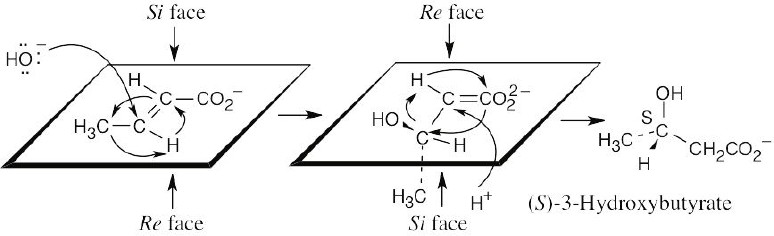
|
| 5.59 |
If you perform the “replacement test” to assign pro-R/pro-S prochirality, you will see that the right “arm” of citrate is pro-R and the product pictured on the right is formed. The pro-S arm is unchanged.

|
| 5.60 |
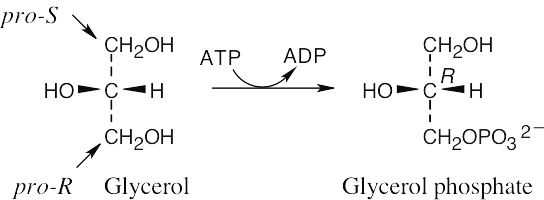 |
| 5.61 |
The reaction removes the pro-R hydrogen.
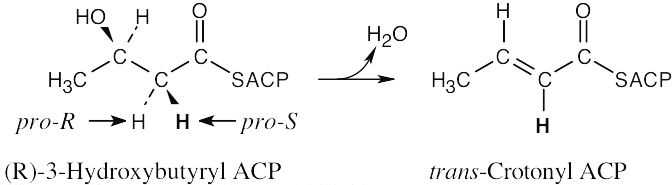
|
General Problems
| 5.62 |

B and C are enantiomers and are optically active. Compound A is their diastereomer and is a meso compound, which is not optically active.
The two isomeric cyclobutane-1,3-dicarboxylic acids are achiral and are optically inactive.
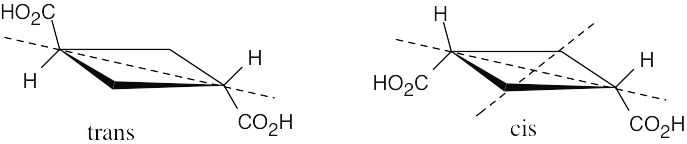
|
| 5.63 |
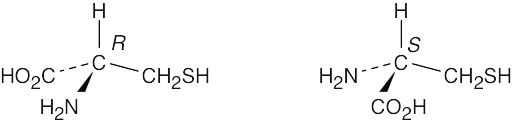 |
| 5.64 |
Cystine has the (S,S) configuration and is optically active.

|
| 5.65 |
(a) |
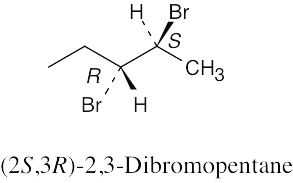 |
|
(b) |
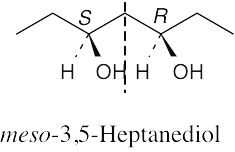 |
| 5.66 |
All chirality centers of Cephalexin have an (R) configuration.
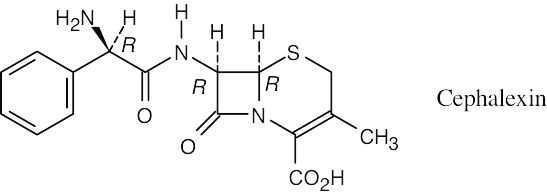
|
| 5.67 |
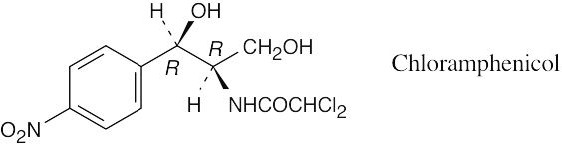 |
| 5.68 |
Mycomycin contains no chiral carbon atoms, yet is chiral. To see why, make a model of mycomycin. For simplicity, call –CH=CHCH=CHCH2CO2H “A” and –C≡CC≡CH “B”. The carbon atoms of an allene have a linear relationship and the π bonds formed are perpendicular to each other. Attach substituents at the sp2 carbons.
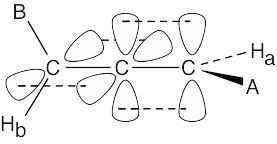
Notice that the substituents A, Ha, and all carbon atoms lie in a plane that is perpendicular to the plane that contains B, Hb, and all carbon atoms.
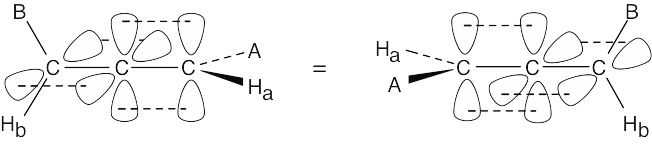
Now, make another model identical to the first, except for an exchange of A and Ha. This new allene is not superimposable on the original allene. The two allenes are enantiomers and are chiral because they possess no plane of symmetry.
|
| 5.69 |
4-Methylcyclohexylideneacetic acid is chiral for the same reason that mycomycin (Problem 5.68) is chiral: It possesses no plane of symmetry and is not superimposable on its mirror image. As in the case of allenes, the two groups at one end of the molecule lie in a plane perpendicular to the plane that contains the two groups at the other end.
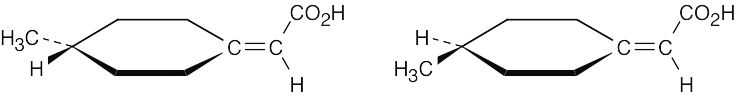
|
| 5.70 |
(a) |
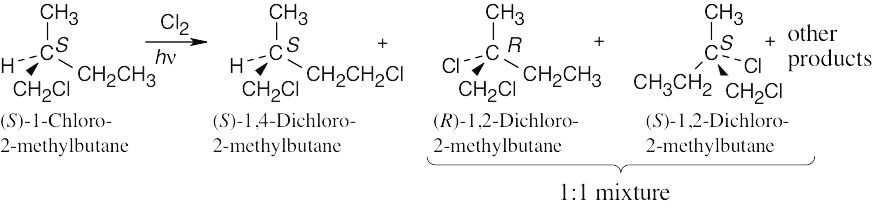 |
|
(b) |
Chlorination at carbon 4 yields an optically active product because the chirality center at C2 is not affected. Chlorination at carbon 2 yields an optically inactive racemic product. |
| 5.71 |
There are four stereoisomers of 2,4-dibromo-3-chloropentane. C and D are enantiomers and are optically active. A and B are optically inactive meso compounds and are diastereomers.
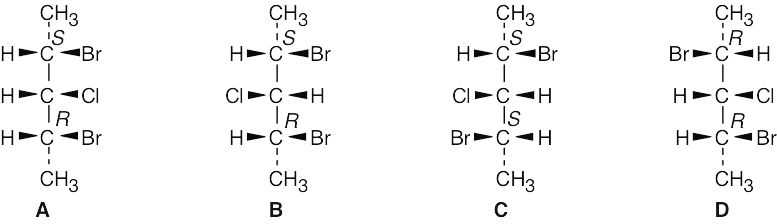
|
| 5.72 |
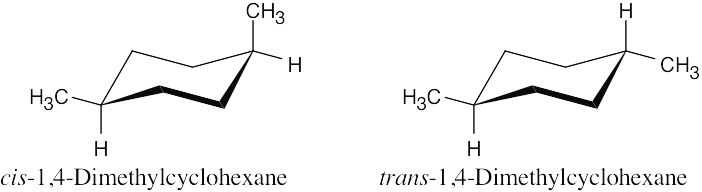 |
|
(a) |
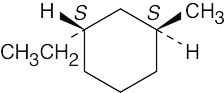
There is only one stereoisomer of each of the 1,4-dimethylcyclohexanes. |
|
(b) |
Neither 1,4-dimethylcyclohexane is chiral. |
|
(c) |
The two 1,4-dimethylcyclohexanes are diastereomers. |
| 5.73 |
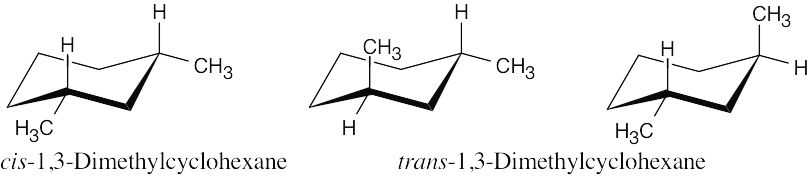 |
|
(a) |
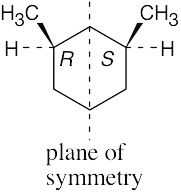
There is one stereoisomer of cis-1,3-dimethylcyclohexane, and there are two stereoisomers of trans-1,3-dimethylcyclohexane. |
|
(b) |
cis-1,3-Dimethylcyclohexane is an achiral meso compound; trans-1,3- dimethylcyclohexane exists as a pair of chiral enantiomers. |
|
(c) |
The two trans stereoisomers are enantiomers, and both are diastereomers of the cis stereoisomer. |
| 5.74 |
The two cis-1,2-dimethylcyclohexane enantiomers rapidly interconvert by a ring flip, leading to an optically inactive 1:1 mixture.
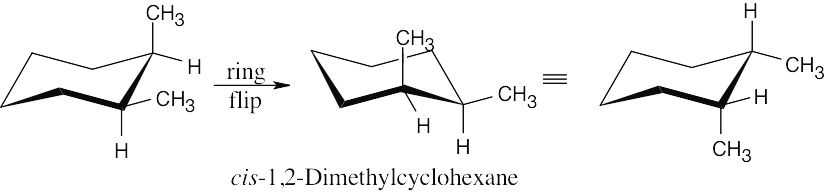
|
| 5.75 |
The product is (R)-2-butanethiol.

|
| 5.76 |
The reaction proceeds by addition of an acetylide anion to the carbonyl group and occurs with equal probability from either face of the planar ketone carbon.
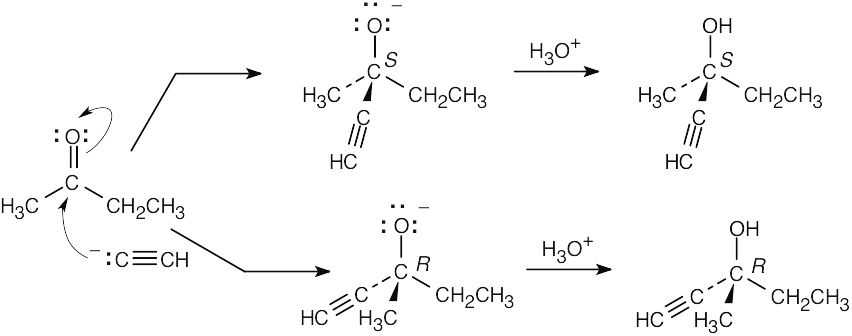
|
|
(a) |
The product is an optically inactive racemic mixture. |
|
(b) |
The two enantiomers are formed in a 50:50 ratio. |
| 5.77 |
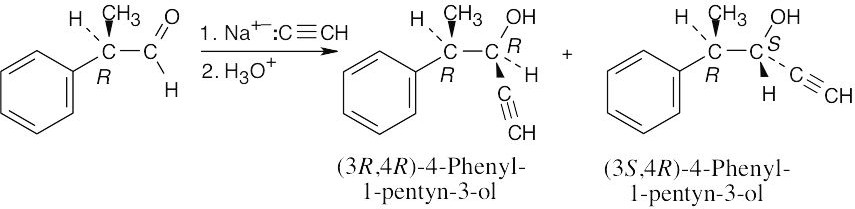 |
|
(a) |
Reaction of sodium acetylide with a chiral aldehyde yields chiral products; the product mixture is optically active. |
|
(b) |
The two products are a mixture of the (3R,4R) and (3S,4R) diastereomers of 4-phenyl-1-pentyn-3-ol. The product ratio can’t be predicted, but it is not 50:50. |
This file is copyright 2023, Rice University. All Rights Reserved.
 and
and 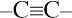 carbons are not chirality centers. By rule 3, all aromatic ring carbons are not chirality centers.
carbons are not chirality centers. By rule 3, all aromatic ring carbons are not chirality centers.