7.5 Strengths of Covalent Bonds
Learning Objectives
By the end of this section, you will be able to:
- Describe the energetics of covalent bond formation and breakage
A bond’s strength describes how strongly each atom is joined to another atom, and therefore how much energy is required to break the bond between the two atoms. In this section, you will learn about the bond strength of covalent bonds.
Bond Strength: Covalent Bonds
Stable molecules exist because covalent bonds hold the atoms together. We measure the strength of a covalent bond by the energy required to break it, that is, the energy necessary to separate the bonded atoms. Separating any pair of bonded atoms requires energy. The stronger a bond, the greater the energy required to break it.
The energy required to break a specific covalent bond in one mole of gaseous molecules is called the bond energy or the bond dissociation energy. The bond energy for a diatomic molecule, DX–Y, is defined as the standard enthalpy change for the endothermic reaction:
For example, the bond energy of the pure covalent H–H bond, DH–H, is 436 kJ per mole of H–H bonds broken:
Molecules with three or more atoms have two or more bonds. The sum of all bond energies in such a molecule is equal to the standard enthalpy change for the endothermic reaction that breaks all the bonds in the molecule. For example, the sum of the four C–H bond energies in CH4, 1660 kJ, is equal to the standard enthalpy change of the reaction:
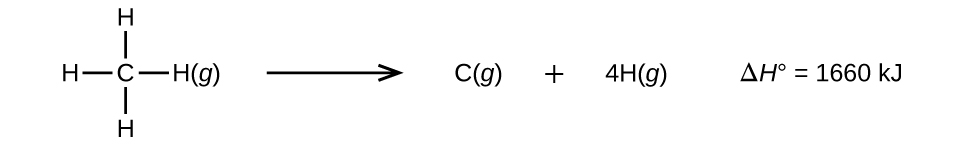
The average C–H bond energy, DC–H, is 1660/4 = 415 kJ/mol because there are four moles of C–H bonds broken per mole of the reaction. Although the four C–H bonds are equivalent in the original molecule, they do not each require the same energy to break; once the first bond is broken (which requires 439 kJ/mol), the remaining bonds are easier to break. The 415 kJ/mol value is the average, not the exact value required to break any one bond.
The strength of a bond between two atoms increases as the number of electron pairs in the bond increases. Generally, as the bond strength increases, the bond length decreases. Thus, we find that triple bonds are stronger and shorter than double bonds between the same two atoms; likewise, double bonds are stronger and shorter than single bonds between the same two atoms. Average bond energies for some common bonds appear in Table 7.2, and a comparison of bond lengths and bond strengths for some common bonds appears in Table 7.3. When one atom bonds to various atoms in a group, the bond strength typically decreases as we move down the group. For example, C–F is 439 kJ/mol, C–Cl is 330 kJ/mol, and C–Br is 275 kJ/mol.
| Bond Energies (kJ/mol) | |||||||
|---|---|---|---|---|---|---|---|
| Bond | Bond Energy | Bond | Bond Energy | Bond | Bond Energy | ||
| H–H | 436 | C–S | 260 | F–Cl | 255 | ||
| H–C | 415 | C–Cl | 330 | F–Br | 235 | ||
| H–N | 390. | C–Br | 275 | Si–Si | 230. | ||
| H–O | 464 | C–I | 240 | Si–P | 215 | ||
| H–F | 569 | N–N | 160 | Si–S | 225 | ||
| H–Si | 395 | N=N | 418 | Si–Cl | 359 | ||
| H–P | 320. | 946 | Si–Br | 290. | |||
| H–S | 340. | N–O | 200 | Si–I | 215 | ||
| H–Cl | 432 | N–F | 270 | P–P | 215 | ||
| H–Br | 370. | N–P | 210 | P–S | 230. | ||
| H–I | 295 | N–Cl | 200 | P–Cl | 330. | ||
| C–C | 345 | N–Br | 245 | P–Br | 270. | ||
| C=C | 611 | O–O | 140 | P–I | 215 | ||
| 837 | O=O | 498 | S–S | 215 | |||
| C–N | 290. | O–F | 160 | S–Cl | 250. | ||
| C=N | 615 | O–Si | 370 | S–Br | 215 | ||
| 891 | O–P | 350 | Cl–Cl | 243 | |||
| C–O | 350. | O–Cl | 205 | Cl–Br | 220. | ||
| C=O | 741 | O–I | 200 | Cl–I | 210. | ||
| 1080. | F–F | 160 | Br–Br | 190. | |||
| C–F | 439 | F–Si | 540 | Br–I | 180. | ||
| C–Si | 360. | F–P | 489 | I–I | 150. | ||
| C–P | 265 | F–S | 285 | ||||
Table 7.2
| Average Bond Lengths and Bond Energies for Some Common Bonds | ||
|---|---|---|
| Bond | Bond Length (Å) | Bond Energy (kJ/mol) |
| C–C | 1.54 | 345 |
| C=C | 1.34 | 611 |
| 1.20 | 837 | |
| C–N | 1.43 | 290. |
| C=N | 1.38 | 615 |
| 1.16 | 891 | |
| C–O | 1.43 | 350. |
| C=O | 1.23 | 741 |
| 1.13 | 1080. | |
Table 7.3
Glossary
- bond energy
- (also, bond dissociation energy) energy required to break a covalent bond in a gaseous substance

