4.9 Describing a Reaction: Intermediates and Catalysts

How can we describe the carbocation formed in the first step of the reaction of ethylene with HBr? The carbocation is clearly different from the reactants, yet it isn’t a transition state and it isn’t a final product.

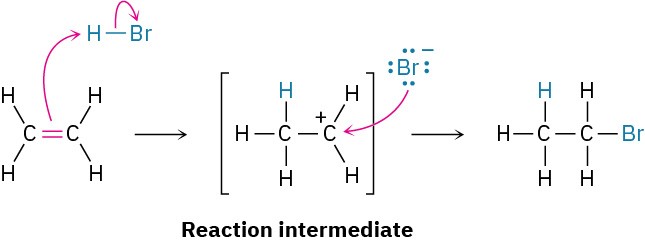We call the carbocation, which exists only transiently during the course of the multistep reaction, a reaction intermediate. As soon as the intermediate is formed in the first step by reaction of ethylene with H⁺, it reacts further with Br⁻ in a second step to give the final product, bromoethane. This second step has its own activation energy (ΔG^‡), its own transition state, and its own energy change (ΔG°). We can picture the second transition state as an activated complex between the electrophilic carbocation intermediate and the nucleophilic bromide anion, in which Br⁻ donates a pair of electrons to the positively charged carbon atom as the new C−Br bond just starts to form.

A complete energy diagram for the overall reaction of ethylene with HBr is shown in Figure 4.11. In essence, we draw a diagram for each of the individual steps and then join them so that the carbocation product of step 1 is the reactant for step 2. As indicated in Figure 4.11, the reaction intermediate lies at an energy minimum between steps. Because the energy level of the intermediate is higher than the level of either the reactant that formed it or the product it yields, the intermediate can’t normally be isolated. It is, however, more stable than its two neighboring transition states.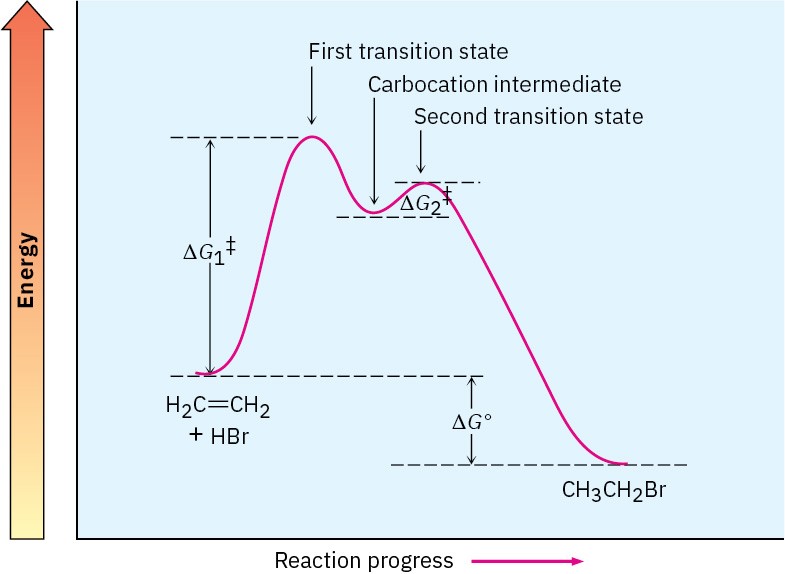Figure 4.11 An energy diagram for the reaction of ethylene with HBr. Two separate steps are involved, each with its own activation energy (ΔG^‡) and free-energy change (ΔG°). The overall ΔG^‡ for the complete reaction is the energy difference between reactants and the highest transition state (which corresponds to ΔG₁^‡ in this case), and the overall ΔG° for the reaction is the energy difference between reactants and final products.

Each step in a multistep process can always be considered separately. Each step has its own ΔG^‡ and its own ΔG°. The overall activation energy that controls the rate of the reaction, however, is the energy difference between initial reactants and the highest transition state, regardless of which step it occurs in. The overall ΔG° of the reaction is the energy difference between reactants and final products.

The biological reactions that take place in living organisms have the same energy requirements as reactions that take place in the laboratory and can be described in similar ways. They are, however, constrained by the fact that they must have low enough activation energies to occur at moderate temperatures, and they must release energy in relatively small amounts to avoid overheating the organism. These constraints can be met through the use of large, structurally complex, enzyme catalysts that alter the mechanism of a reaction to a pathway that can proceed through a series of small steps rather than one or two large steps. Thus, an energy diagram for a biological reaction might look like that in Figure 4.12.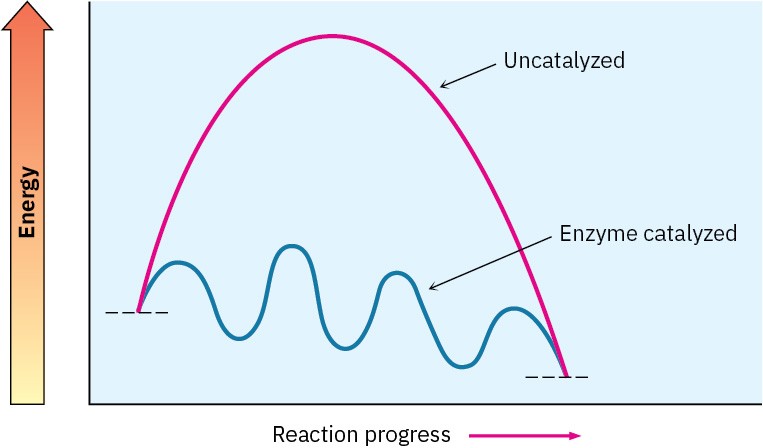Figure 4.12 Energy diagrams for a typical, enzyme-catalyzed biological reaction and an uncatalyzed laboratory reaction. The biological reaction involves many steps, each of which has a relatively small activation energy and small energy change. The end result is the same, however.

Worked Example 4.3: Drawing a Reaction Energy Diagram

Sketch an energy diagram for a one-step reaction that is fast and highly exergonic.

Strategy

A fast reaction has a small ΔG^‡, and a highly exergonic reaction has a large negative ΔG°.

Solution

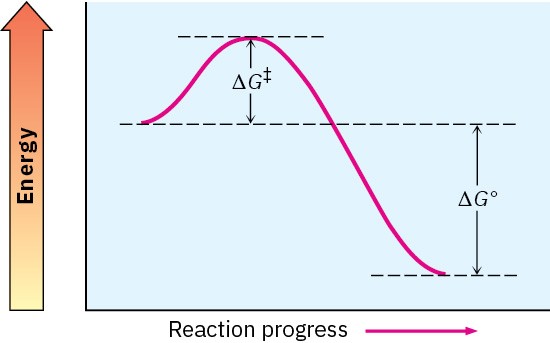Worked Example 4.4: Drawing a Reaction Energy Diagram

Sketch an energy diagram for a two-step exergonic reaction whose second step has a higher-energy transition state than its first step. Show ΔG^‡ and ΔG° for the overall reaction.

Strategy

A two-step reaction has two transition states and an intermediate between them. The ΔG^‡ for the overall reaction is the energy change between reactants and the highest-energy transition state—the second one in this case. An exergonic reaction has a negative overall ΔG°.

Solution

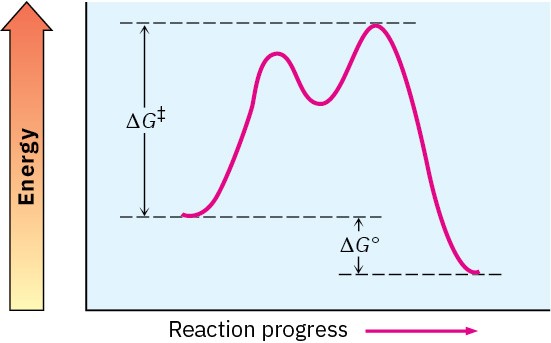Problem 4.19
Sketch an energy diagram for a two-step reaction in which both steps are exergonic and in which the second step has a higher-energy transition state than the first. Label the parts of the diagram corresponding to reactant, product, intermediate, overall ΔG^‡, and overall ΔG°.