1.5 Describing Chemical Bonds: Valence Bond Theory
How does electron sharing lead to bonding between atoms? Two models have been developed to describe covalent bonding: valence bond theory and molecular orbital theory. Each model has its strengths and weaknesses, and chemists tend to use them interchangeably depending on the circumstances. Valence bond theory is the more easily visualized of the two, so most of the descriptions we’ll use in this book derive from that approach.
According to valence bond (VB) theory, a covalent bond forms when two atoms approach each other closely and a singly occupied orbital on one atom overlaps a singly occupied orbital on the other atom. The electrons are now paired in the overlapping orbitals and are attracted to the nuclei of both atoms, thus bonding the atoms together. In the H2 molecule, for instance, the H–H bond results from the overlap of two singly occupied hydrogen 1s orbitals.
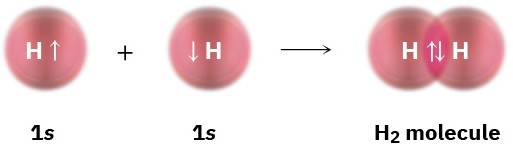
The overlapping orbitals in the H2 molecule have the elongated egg shape we might get by pressing two spheres together. If a plane were to pass through the middle of the bond, the intersection of the plane and the overlapping orbitals would be a circle. In other words, the H–H bond is cylindrically symmetrical, as shown in Figure 1.9. Such bonds, which are formed by the head-on overlap of two atomic orbitals along a line drawn between the nuclei, are called sigma (σ) bonds.
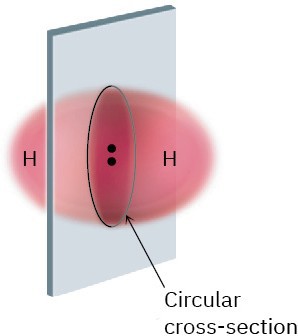Figure 1.9 The cylindrical symmetry of the H–H σ bond in an H2 molecule. The intersection of a plane cutting through the σ bond is a circle.
During the bond-forming reaction 2H· ⟶ H2, 436 kJ/mol (104 kcal/mol) of energy is released. Because the product H2 molecule has 436 kJ/mol less energy than the starting 2 H· atoms, the product is more stable than the reactant and we say that the H–H bond has a bond strength of 436 kJ/mol. In other words, we would have to put 436 kJ/mol of energy into the H–H bond to break the H2 molecule apart into two H atoms (Figure 1.10). For convenience, we’ll generally give energies in both kilocalories (kcal) and the SI unit kilojoules (kJ): 1 kJ = 0.2390 kcal; 1 kcal = 4.184 kJ.
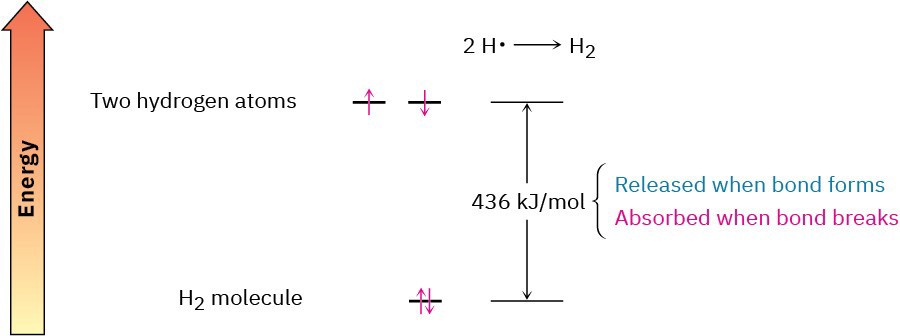Figure 1.10 Relative energy levels of two H atoms and the H2 molecule. The H2 molecule has 436 kJ/mol (104 kcal/mol) less energy than the two separate H atoms, so 436 kJ/mol of energy is released when the H–H bond forms. Conversely, 436 kJ/mol is absorbed when the H–H bond breaks.
How close are the two nuclei in the H2 molecule? If they are too close, they will repel each other because both are positively charged. Yet if they’re too far apart, they won’t be able to share the bonding electrons. Thus, there is an optimum distance between nuclei that leads to maximum stability (Figure 1.11). Called the bond length, this distance is 74 pm in the H– H molecule. Every covalent bond has both a characteristic bond strength and bond length.
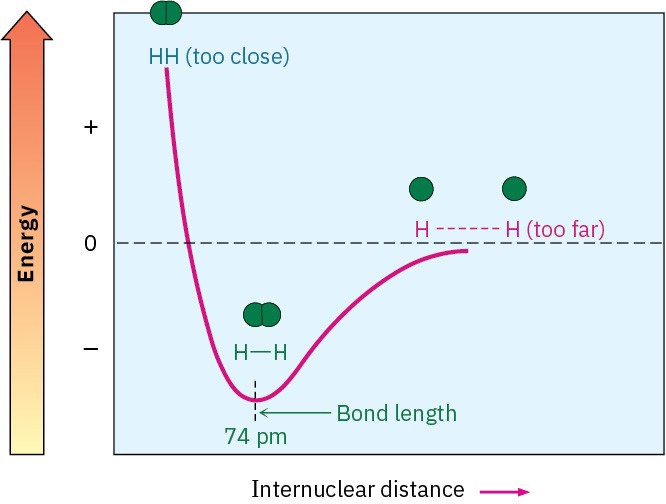Figure 1.11 A plot of energy versus internuclear distance for two hydrogen atoms. The distance between nuclei at the minimum energy point is the bond length.
