24.5 Biological Amines and the Henderson–Hasselbalch Equation

We saw in Section 20.3 that the extent of dissociation of a carboxylic acid HA in an aqueous solution buffered to a given pH can be calculated with the Henderson–Hasselbalch equation. Furthermore, we concluded that at the physiological pH of 7.3 inside living cells, carboxylic acids are almost entirely dissociated into their carboxylate anions, RCO2–.

Henderson–Hasselbalch equation:

[A^–][A^–]

pH = p𝐾a + log [HA]solog [HA] = pH – p𝐾a

What about amine bases? In what form do they exist at physiological pH? As the amine (A–

= RNH2), or as the ammonium ion (HA = RNH3+)? Let’s take a 0.0010 M solution of methylamine at pH = 7.3, for example. According to Table 24.1, the pKa of methylammonium ion is 10.64, so from the Henderson–Hasselbalch equation, we have

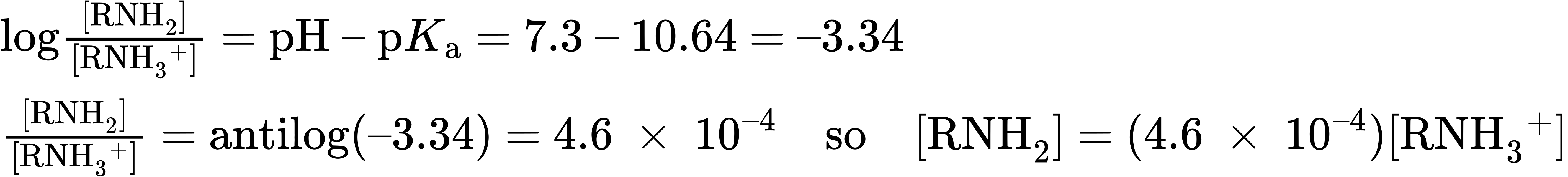
In addition, we know that

[RNH2] + [RNH3+] = 0.0010 M

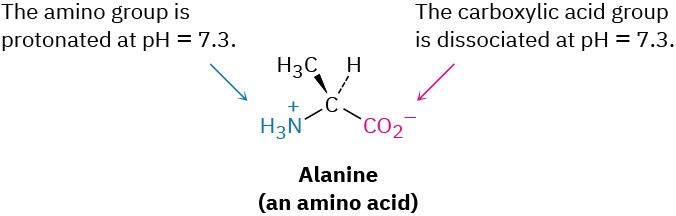
Solving the two simultaneous equations gives [RNH3+] = 0.0010 M and [RNH2] = 5 × 10–7 M. In other words, at a physiological pH of 7.3, essentially 100% of the methylamine in a 0.0010 M solution exists in its protonated form as methylammonium ion. The same is true of other amine bases, so we always write cellular amines in their protonated form and amino acids in their ammonium carboxylate form to reflect their structures at physiological pH.

Problem 24-7

Calculate the percentages of neutral and protonated forms present in a solution of 0.0010 Molar pyrimidine at pH = 7.3. The pKa of pyrimidinium ion is 1.3.