13.12 DEPT 13C NMR Spectroscopy
Numerous techniques developed in recent years have made it possible to obtain enormous amounts of information from 13C NMR spectra. Among these techniques is one called DEPT–NMR, for distortionless enhancement by polarization transfer, which makes it possible to distinguish between signals due to CH3, CH2, CH, and quaternary carbons. That is, the number of hydrogens attached to each carbon in a molecule can be determined.
A DEPT experiment is usually done in three stages, as shown in Figure 13.21 for 6-methyl- 5-hepten-2-ol. The first stage is to run an ordinary spectrum (called a broadband- decoupled spectrum) to locate the chemical shifts of all carbons. Next, a second spectrum called a DEPT-90 is run, using special conditions under which only signals due to CH carbons appear. Signals due to CH3, CH2, and quaternary carbons are absent. Finally, a third spectrum called a DEPT-135 is run, using conditions under which CH3 and CH resonances appear as positive signals, CH2 resonances appear as negative signals—that is, as peaks below the baseline—and quaternary carbons are again absent.
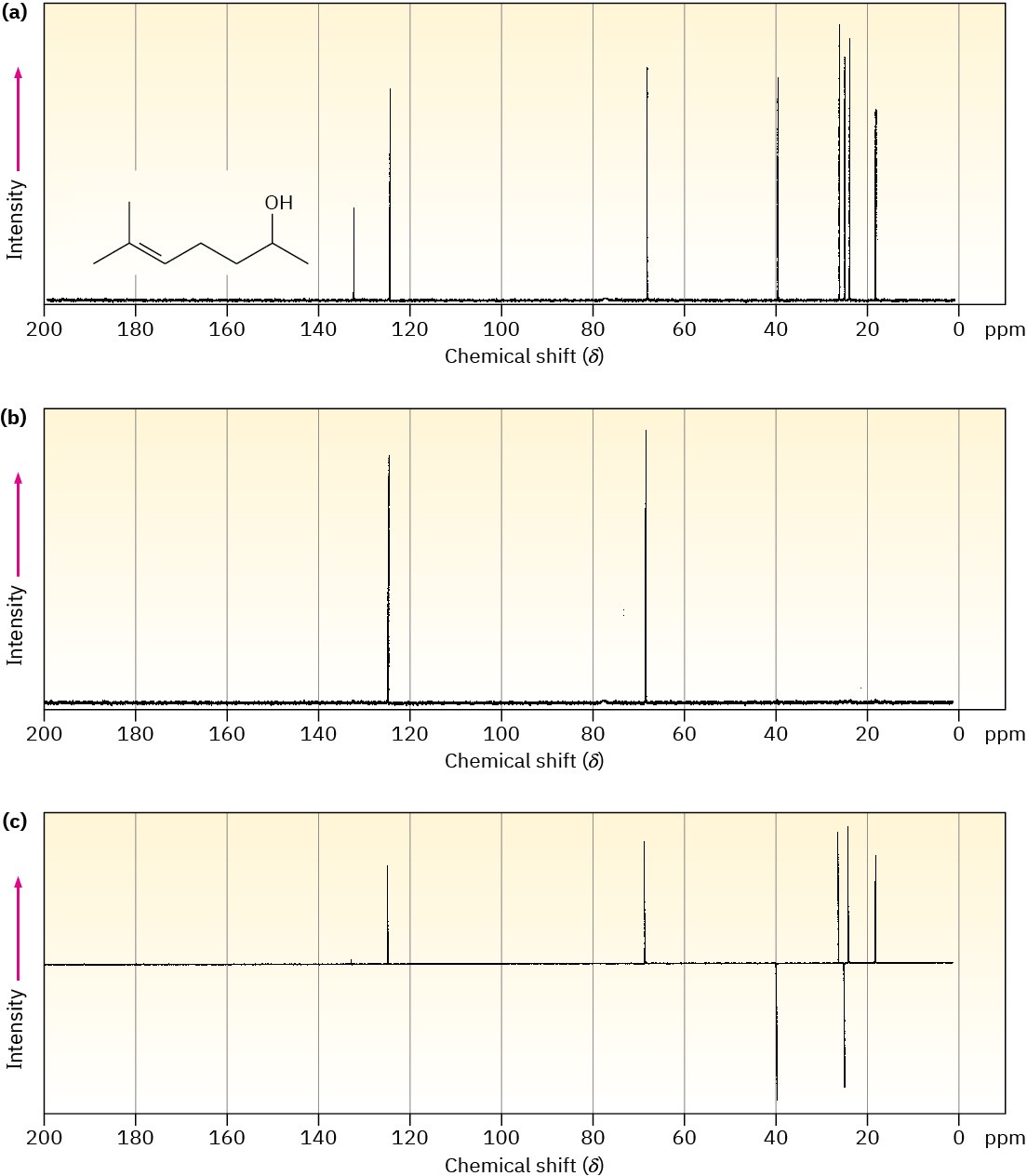
Figure 13.21 DEPT–NMR spectra for 6-methyl-5-hepten-2-ol. Part (a) is an ordinary broadband-decoupled spectrum, which shows signals for all eight carbons. Part (b) is a DEPT-90 spectrum, which shows only signals for the two CH carbons. Part (c) is a DEPT- 135 spectrum, which shows positive signals for the two CH and three CH3 carbons and negative signals for the two CH2 carbons.
Putting together the information from all three spectra makes it possible to tell the number of hydrogens attached to each carbon. The CH carbons are identified in the DEPT-90 spectrum, the CH2 carbons are identified as negative peaks in the DEPT-135 spectrum, the CH3 carbons are identified by subtracting the CH peaks from the positive peaks in the DEPT-135 spectrum, and quaternary carbons are identified by subtracting all peaks in the DEPT-135 spectrum from the peaks in the broadband-decoupled spectrum.
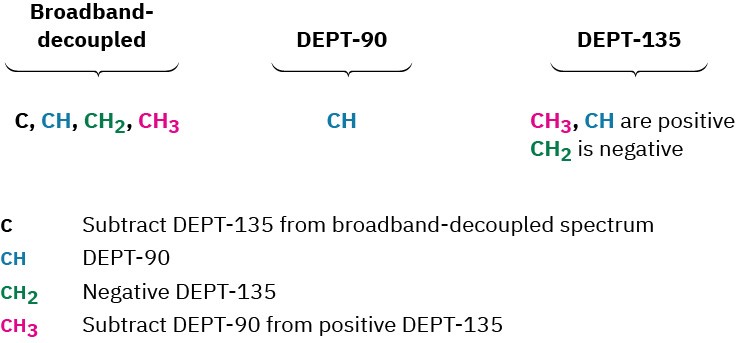
Worked Example 13.4Assigning a Chemical Structure from a 13C NMR SpectrumPropose a structure for an alcohol, C4H10O, that has the following 13C NMR spectral data:
Broadband decoupled 13C NMR: 19.0, 31.7, 69.5 δ;
DEPT-90: 31.7 δ;
DEPT-135: positive peak at 19.0 δ, negative peak at 69.5 δ.
StrategyAs noted in Section 7.2, it usually helps with compounds of known formula but unknown structure to calculate the compound’s degree of unsaturation. In the present instance, a formula of C4H10O corresponds to a saturated, open-chain molecule.To gain information from the 13C data, let’s begin by noting that the unknown alcohol has four carbon atoms, yet has only three NMR absorptions, which implies that two of the carbons must be equivalent. Looking at chemical shifts, two of the absorptions are in the typical alkane region (19.0 and 31.7 δ), while one is in the region of a carbon bonded to an electronegative atom (69.5 δ)—oxygen in this instance. The DEPT-90 spectrum tells us that the alkyl carbon at 31.7 δ is tertiary (CH); the DEPT-135 spectrum tells us that the alkyl carbon at 19.0 δ is a methyl (CH3) and that the carbon bonded to oxygen (69.5 δ) is secondary (CH2). The two equivalent carbons are probably both methyls bonded to the same tertiary carbon, (CH3)2CH–. We can now put the pieces together to propose a structure: 2-methyl-1-propanol.Solution
Problem 13-20
Assign a chemical shift to each carbon in 6-methyl-5-hepten-2-ol (Figure 13.21). Problem 13-21
Estimate the chemical shift of each carbon in the following molecule. Predict which carbons will appear in the DEPT-90 spectrum, which will give positive peaks in the DEPT-135 spectrum, and which will give negative peaks in the DEPT-135 spectrum.
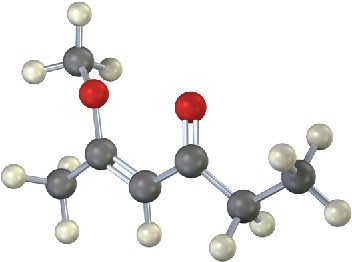
Problem 13-22
Propose a structure for an aromatic hydrocarbon, C11H16, that has the following 13C NMR spectral data:
- Broadband decoupled: 29.5, 31.8, 50.2, 125.5, 127.5, 130.3, 139.8 δ
- DEPT-90: 125.5, 127.5, 130.3 δ
- DEPT-135: positive peaks at 29.5, 125.5, 127.5, 130.3 δ; negative peak at 50.2 δ

