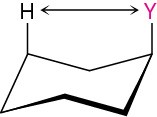
4.7 Conformations of Monosubstituted Cyclohexanes

Even though cyclohexane rings flip rapidly between chair conformations at room temperature, the two conformations of a monosubstituted cyclohexane aren’t equally stable. In methylcyclohexane, for instance, the equatorial conformation is more stable than the axial conformation by 7.6 kJ/mol (1.8 kcal/mol). The same is true of other monosubstituted cyclohexanes: a substituent is almost always more stable in an equatorial position than in an axial position.

You might recall from your general chemistry course that it’s possible to calculate the percentages of two isomers at equilibrium using the equation ΔE = –RT ln K, where ΔE is the energy difference between isomers, R is the gas constant [8.315 J/(K·mol)], T is the Kelvin temperature, and K is the equilibrium constant between isomers. For example, an energy difference of 7.6 kJ/mol means that about 95% of methylcyclohexane molecules have an equatorial methyl group at any given instant while only 5% have an axial methyl group. Figure 4.13 plots the relationship between energy and isomer percentages.

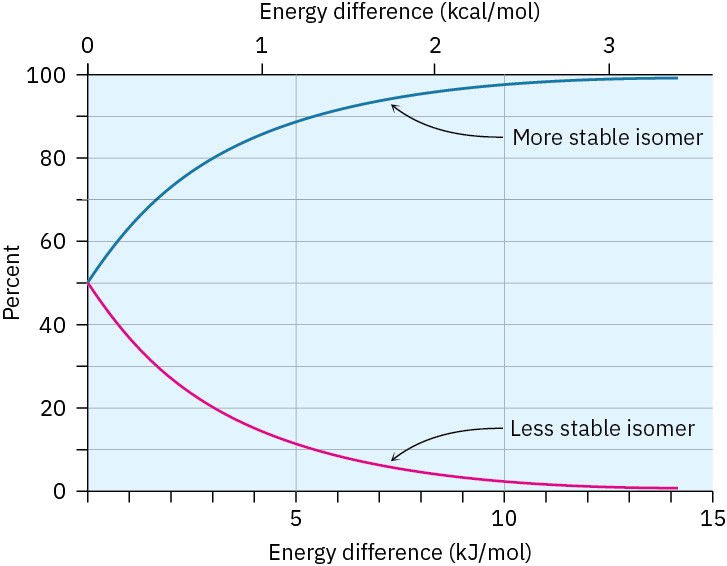
Figure 4.13 A plot of the percentages of two isomers at equilibrium versus the energy difference between them. The curves are calculated using the equation ΔE = −RT ln K.

The energy difference between axial and equatorial conformations is due to steric strain caused by 1,3-diaxial interactions. The axial methyl group on C1 is too close to the axial hydrogens three carbons away on C3 and C5, resulting in 7.6 kJ/mol of steric strain (Figure 4.14).

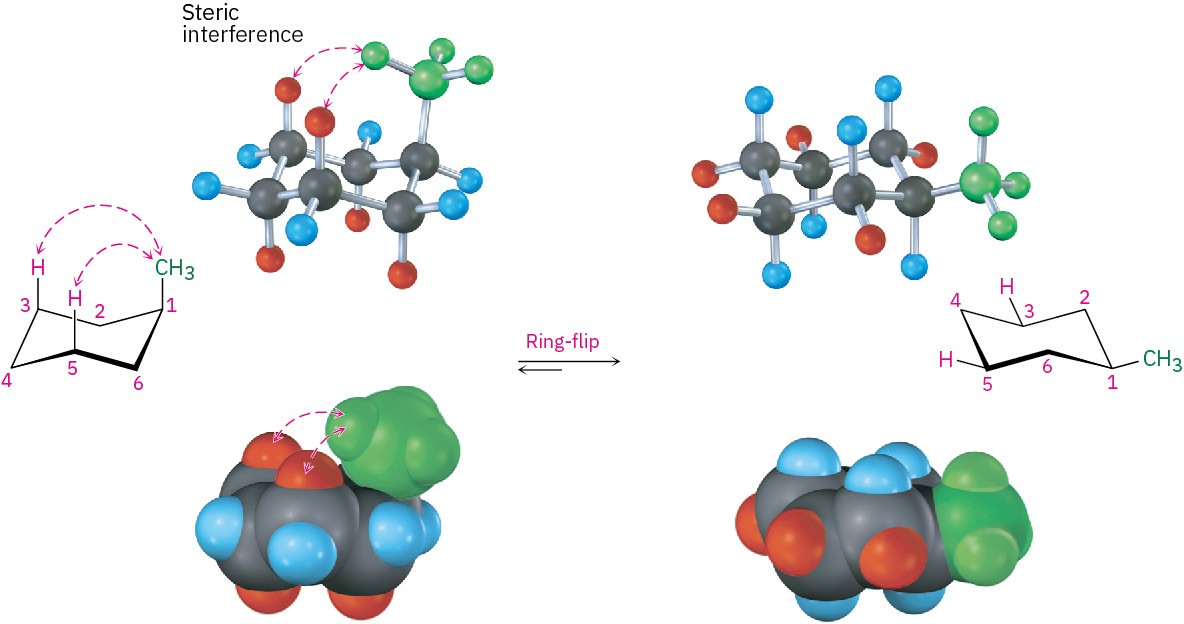
Figure 4.14 Interconversion of axial and equatorial methylcyclohexane, represented in several formats. The equatorial conformation is more stable than the axial conformation by 7.6 kJ/mol.

The 1,3-diaxial steric strain in substituted methylcyclohexane is already familiar—we saw it previously as the steric strain between methyl groups in gauche in Section 3.7. Gauche butane is less stable than anti butane by 3.8 kJ/mol (0.9 kcal/mol) because of steric interference between hydrogen atoms on the two methyl groups. Comparing a four-carbon fragment of axial methylcyclohexane with gauche butane shows that the steric interaction is the same in both (Figure 4.15). Because axial methylcyclohexane has two such interactions, it has 2 × 3.8 = 7.6 kJ/mol of steric strain. Equatorial methylcyclohexane has no such interactions and is therefore more stable.

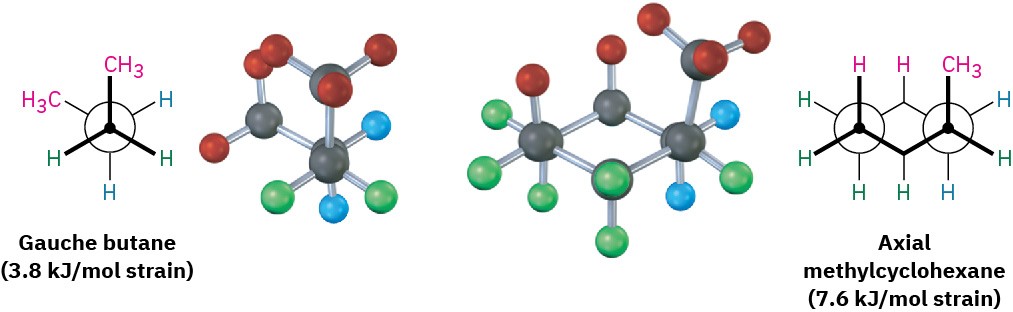
Figure 4.15 The origin of 1,3-diaxial interactions in methylcyclohexane. The steric strain between an axial methyl group and an axial hydrogen atom three carbons away is identical to the steric strain in gauche butane. (To display clearly the diaxial interactions in methylcyclohexane, two of the equatorial hydrogens are not shown.)

The exact amount of 1,3-diaxial steric strain in a given substituted cyclohexane depends on the nature and size of the substituent, as indicated in Table 4.1. Not surprisingly, the

amount of steric strain increases through the series H3C− < CH3CH2− < (CH3)2CH–<< (CH3)3C−, paralleling the increasing size of the alkyl groups. Note that the values given in Table 4.1 refer to 1,3-diaxial interactions of the substituent with a single hydrogen atom. These values must be doubled to arrive at the amount of strain in a monosubstituted cyclohexane.

Table 4.1 Steric Strain in Monosubstituted Cyclohexanes

Problem 4-15

What is the energy difference between the axial and equatorial conformations of cyclohexanol (hydroxycyclohexane)?

Problem 4-16

Why do you suppose an axial cyano (–CN) substituent causes practically no 1,3-diaxial steric strain (0.4 kJ/mol)?

Problem 4-17

Look back at Figure 4.13 and estimate the percentages of axial and equatorial conformations present at equilibrium in bromocyclohexane.