13.1 Nuclear Magnetic Resonance Spectroscopy

Many kinds of nuclei behave as if they were spinning about an axis, somewhat as the earth spins daily. Because they’re positively charged, these spinning nuclei act like tiny magnets and can interact with an external magnetic field, denoted B0. Not all nuclei act this way, but fortunately for organic chemists, both the proton (1H) and the 13C nucleus do have spins.

The more common 12C isotope, however, does not have nuclear spin. (In speaking about NMR, the words proton and hydrogen are often used interchangeably, since a hydrogen nucleus is just a proton.) Let’s see what the consequences of nuclear spin are and how we can use the results.

In the absence of an external magnetic field, the spins of magnetic nuclei are oriented randomly. When a sample containing these nuclei is placed between the poles of a strong magnet, however, the nuclei adopt specific orientations, much as a compass needle orients in the earth’s magnetic field. A spinning 1H or 13C nucleus can orient so that its own tiny magnetic field is aligned either with (parallel to) or against (antiparallel to) the external field. The two orientations don’t have the same energy, however, and aren’t equally likely. The parallel orientation is slightly lower in energy by an amount that depends on the strength of the external field, making this spin state very slightly favored over the antiparallel orientation (Figure 13.2).

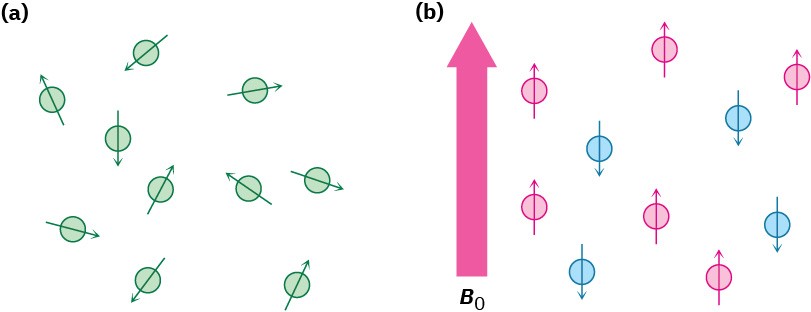
Figure 13.2 (a) Nuclear spins are oriented randomly in the absence of an external magnetic field but (b) have a specific orientation in the presence of an external field, B0. Some of the spins (red) are aligned parallel to the external field while others (blue) are antiparallel. The parallel spin state is slightly lower in energy and therefore favored.

If the oriented nuclei are irradiated with electromagnetic radiation of the proper frequency, energy absorption occurs and the lower-energy spin state “flips” to the higher-energy state. When this spin-flip occurs, the magnetic nuclei are said to be in resonance with the applied radiation—hence the name nuclear magnetic resonance.

The exact frequency necessary for resonance depends both on the strength of the external magnetic field, the identity of the nucleus, and the electronic environment of the nucleus. If a very strong magnetic field is applied, the energy difference between the two spin states is larger and higher-frequency (higher-energy) radiation is required for a spin-flip. If a

weaker magnetic field is applied, less energy is required to effect the transition between nuclear spin states (Figure 13.3).

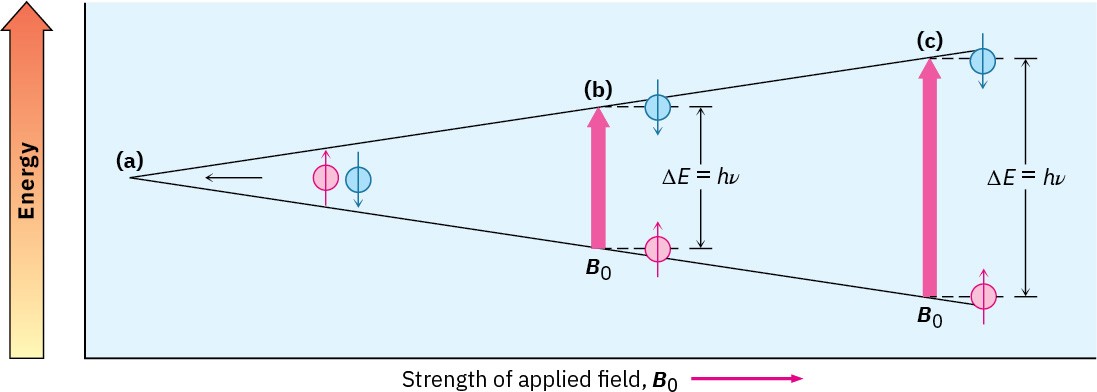
Figure 13.3 The energy difference ΔE between nuclear spin states depends on the strength of the applied magnetic field. Absorption of energy with frequency ν converts a nucleus from a lower spin state to a higher spin state. (a) Spin states have equal energies in the absence of an applied magnetic field but (b) have unequal energies in the presence of a magnetic field. At ν = 200 MHz, ∆E = 8.0 × 10–5 kJ/mol (1.9 × 10–5 kcal/mol). (c) The energy difference between spin states is greater at larger applied fields. At ν = 500 MHz, ∆E = 2.0 × 10–4 kJ/mol.

In practice, superconducting magnets that produce enormously powerful fields up to 23.5 tesla (T) are sometimes used, but field strengths in the range of 4.7 to 7.0 T are more common. At a magnetic field strength of 4.7 T, so-called radiofrequency (rf) energy in the 200 MHz range (1 MHz = 106 Hz) brings a 1H nucleus into resonance, and rf energy of 50 MHz brings a 13C nucleus into resonance. At the highest field strength currently available in commercial instruments (23.5 T), 1000 MHz energy is required for 1H spectroscopy. These energies needed for NMR are much smaller than those required for IR spectroscopy; 200 MHz rf energy corresponds to only 8.0 × 10–5 kJ/mol versus the 4.8 to 48 kJ/mol needed for IR spectroscopy.

1H and 13C nuclei are not unique in their ability to exhibit the NMR phenomenon. All nuclei with an odd number of protons (1H, 2H, 14N, 19F, 31P, for example) and all nuclei with an odd number of neutrons (13C, for example) show magnetic properties. Only nuclei with even numbers of both protons and neutrons (12C, 16O, 32S) do not give rise to magnetic phenomena (Table 13.1).

Table 13.1 The NMR Behavior of Some Common Nuclei

Problem 13-1

The amount of energy required to spin-flip a nucleus depends both on the strength of the external magnetic field and on the nucleus. At a field strength of 4.7 T, rf energy of 200 MHz is required to bring a 1H nucleus into resonance, but energy of only 187 MHz will bring a

19F nucleus into resonance. Calculate the amount of energy required to spin-flip a 19F

nucleus. Is this amount greater or less than that required to spin-flip a 1H nucleus? Problem 13-2

Calculate the amount of energy required to spin-flip a proton in a spectrometer operating at 300 MHz. Does increasing the spectrometer frequency from 200 to 300 MHz increase or decrease the amount of energy necessary for resonance?